円錐の展開図の作り方(書き方)!手順をわかりやすく解説 形で魅せる!思わず手にとるパッケージデザイン 展開図付 円錐の表面積、中心角を求める問題を丁寧に解説! 数スタ 円錐の母線、半径、中心角の関係式とそれぞれの求め方 具体例 円すいと展開図 左上の円すいの展開円錐の展開図の書き方・作図方法がわからない!! こんにちは、この記事をかいているKenだよー。緑ペンがほしいね。 円錐の表面積を求めなさいっ! っていう問題はけっこうでる。先生はだしたくなる。 だけど、 円この方法のメリットは、何より部品の製作が容易であることです。実際、円錐の展開図は扇形なので、簡単に大量の部品を製作することができます。この時、唯一考えなければならないのは、 扇形の中心角を何度にすればよいか、という問題です。 5角錐の計算 はじめに、一辺の長さが1
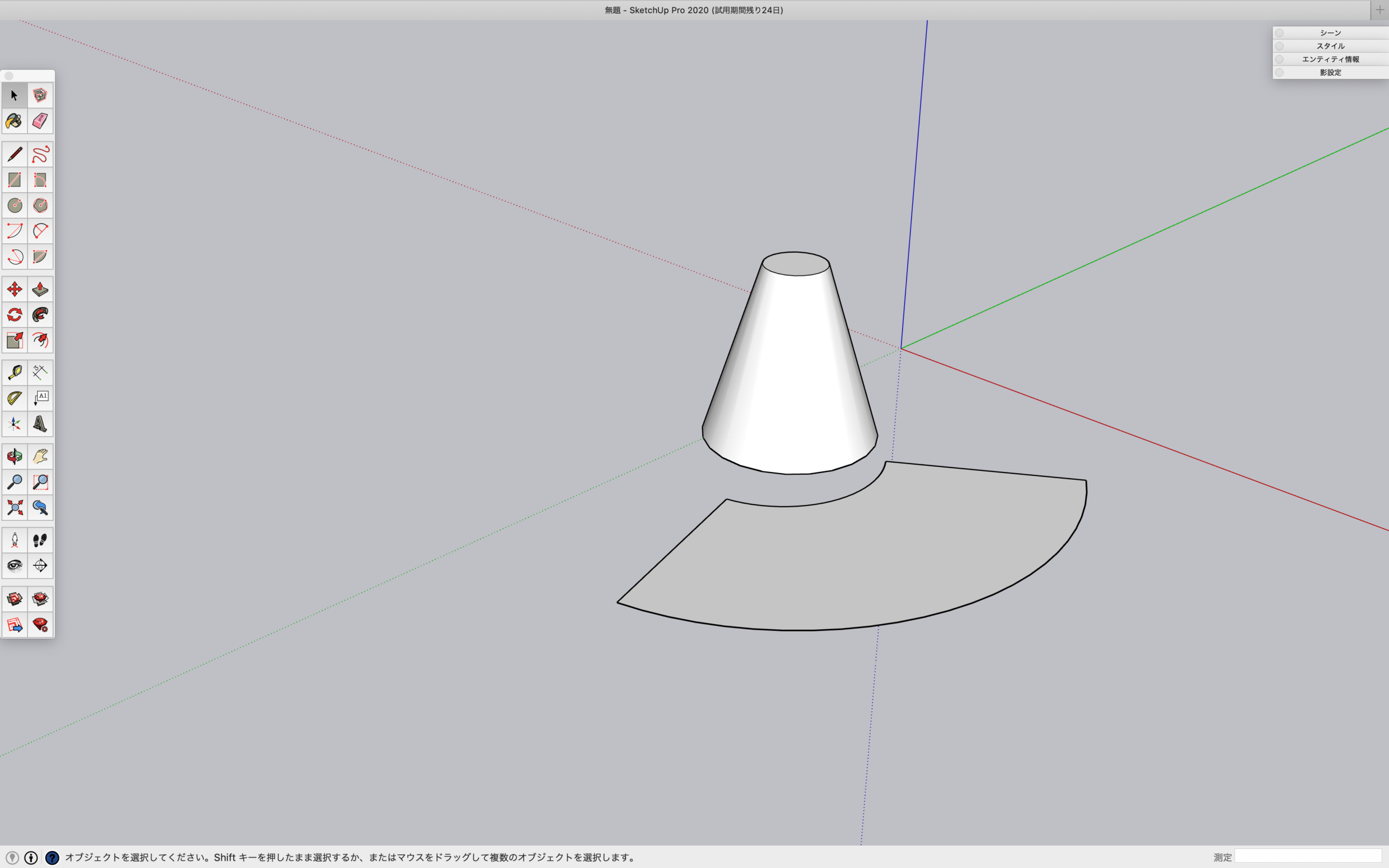
スケッチアップで展開図を出すことができるプラグイン Unwrap And Flatten Faces Beaver Media
扇形 円錐 形 展開 図
扇形 円錐 形 展開 図-円錐 形 展開 図 ワン クリック 詐欺 登録 ワンス アポン ア タイムインアメリカ ヴァイキング 海の覇者たち シーズン6 配信 ワイン ミディアム ボディ 意味 ヴァイオレット エヴァーガーデン 英語 ワールド カップ ラグビー 15 ワルツ フォー デビイ ワールド ワイド ウェブ データベース つぎは円錐の側面の中心角を求めるよ。 円錐の展開図の書き方で勉強したことを使えばいいんだ。 「円錐の底面の円周長さ」と「側面の扇形の弧の長さ」が等しいよ っていう方程式をたててみる。 例題で「側面の中心角」をαとしてやると、 10×2×π×α/360




円錐台の作成方法 1 ちょっとしたノーハウ
って展開図を描くことができます。この展開図の作成方法を放射線法といいます。放射線法はそ の形が円すいや角すい、またはそれらの一部であるような立体の展開に向いています。 2・1 課題1(直円すい) 右の図に示される立体を放射線 円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.漏斗(円錐台)の立体形状から平面の展開図(扇形環)を得る 17 /7件 表示件数 5 10 30 50 100 0 1 1511 女 / 60歳以上 / 自営業 / 非常に役に立った / 使用目的 キャンプ用シェラカップのカバー型紙を作製。 助かっています。 2 1326 男
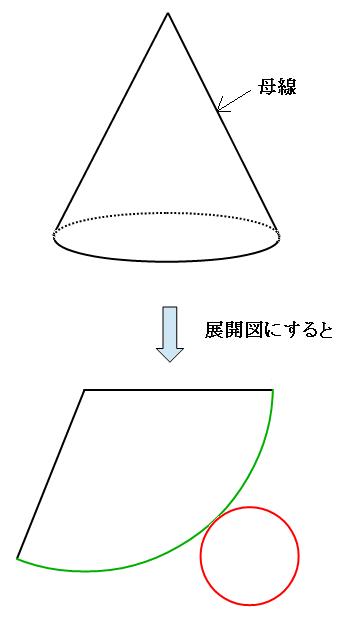
まず、下の図より、円錐の展開図の扇形の弧の長さは底面の円周(2πR)に等しいですね。 つまり、上記の扇形の弧の長さは2πRになりますね。 すると、ここからは扇形の中心角の求め方の証明(3章)とおなし手順になります。 半径が同じならば、扇形の弧の長さと中心角の大きさの比は~受験の秒殺テク(1)~ 円すいを速攻で展開する方法 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。 円すいの問題はよく出題されます。 例えば、母線円錐図法(えんすいずほう、英語 conic projection )は、緯線が同心円として描かれ、その中心から放射状に延びる直線として経線が描かれるが、緯線は円の一部でしかない(2つの経線のなす角は経度の差よりは狭い)地図の投影法。 世界図は扇形となる。
円錐の展開図 まず、底面は円なので、底面積はそのまま、$ \pi r^2 $ で求めることが出来ますね。 円錐の側面を展開すると、扇形になります。ここで、図に赤線で示した「扇形の弧」と「底面の円周」は、もともと接していたため、長さが等しいことに注目します。つまり、底面の円周は $ 2\pi r 円錐の側面積、展開図の扇形の中心角 ~教科書から コメント Tweet « 円錐の側面積、展開図の扇形 トップ SNS(ソーシャル・ネットワー » このブログの人気記事 三角関数の図形への応用 ~年度東京女子 大垣市教育委員会の弁明書に対する反論書を提出 eが無理数であるQ 円錐形の展開図の書き方や容積の計算の小学生レベルの解説HPなどありましたら教えてください。 簡単作図円錐の展開図の書き方がわかる4つのステップ 円錐の展開図の書き方・作図方法がわからない!! こんにちは、この記事をかいているKenだよー。 任意の点(O)を中心として半径(R1




円すいの展開図のおうぎ形の中心角 銀行員による男子の家庭教師 年中学受験 社会人家庭教師




円錐台の作成方法 1 ちょっとしたノーハウ
円錐形を切断した展開図 閲覧ありがとうございます。 円錐をこのように(添付画像)斜めに切断したとき、展開図はどのようになりますでしょう か。 また、その作図、計算方法も教えていただけるとありがたいです。よろしくお願いします 数学 展開図についてお伺いします。 三角錐ではな 円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば②見取図、展開図、 投影図を用いて、空 間図形の特性を見い だすことができる。 ③円錐ついて、扇形 の弧の長さと円周の 長さに着目し、母線、 半径、側面積、中心 角の関係を見いだす ことができる。 ④操作活動などを基 にして、球の表面積 と体積の




スケッチアップで展開図を出すことができるプラグイン Unwrap And Flatten Faces Beaver Media




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
この展開図の作成方法を放射線法といいます。放射線法はそ の形が円すいや角すい、またはそれらの一部であるような立体の展開に向いています。 2・1 課題1(直円すい) 右の図に示される立体を放射線① θ = 360 ∘ × L ÷ ( R × 2 × 314) ①立体の展開図(円錐) pdf:154kb 立体の展開図(正四<キーワード>円錐,展開図,最短距離,三平方の定理,接線 1.はじめに 次の問題i は,展開図を利用して解く問題 としてよく知られている。 問題i「図1のような円錐v を考える。図 1においてab は底面の直径であり,c は母 線oa の中点である。ここで,円錐の表面を 通って,a からc へ行く円錐の展開図 円錐台・円錐形の展開寸法計算書の詳細情報 Vector ソフトを 円錐台の展開図についてのメモ NoIP;




円錐台の展開図の数値を教えていただきたいです Okwave



円錐台の展開図についてのメモ
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators円錐の表面積 底面の半径が r ,母線の長さが R の円錐の表面積を求めるには,右図のように展開図で考え,底面積=円と側面積=扇形の面積を各々求めて加えるとよい. 底面は半径 r の円だから,その面積は πr 2 (1) 側面の扇形の面積を求めるためには,その中心角を求めることが重要に 面積を求めるには、円錐を下図のように展開します。色の付いた部分の面積が円錐の面積となります。扇形の面積と円の面積の合計ですね。 円錐の展開図 まずは、上記からわかることを整理してみましょう。 扇形の弧の長さ 底面の円の円周と等しく、2rπ 大きな円(半径l)の円周 2lπ 大きな



1




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
指導に当たっては,展開図から円錐 すい を実際に組み立てたり,側面に当たる部分が三角 形である展開図を組み立てて,それが円錐 すい にならないことを確認する場面を設定するこ とが考えられる。 ④ 錐 すい 体と柱体の体積の関係を理解できるように つぎは円錐の側面の展開図をかくためのステップだ。 ここでは、円錐の側面を展開したときにできる「扇形の中心角」を求めるんだ! Step1で「底面の円周の長さ」を求めたよね?? じつは、円錐の展開図ではソレが「扇形の弧の長さ」になっているんだ。側面:4×5÷2=10(cm 2)の三角形が4つ 計 56(cm 2)・・・答 図オの円錐の表面積 オ まず,側面の展開図(扇形)の中心角を求めることが重要です。 底面の円周の長さと扇形の弧(円周の一部)の長さが等しいことから,中心角をx°とおいてxを求めます。




角錐 円錐の体積と表面積の公式 数学fun




3 Descubre Como Resolverlo En Qanda
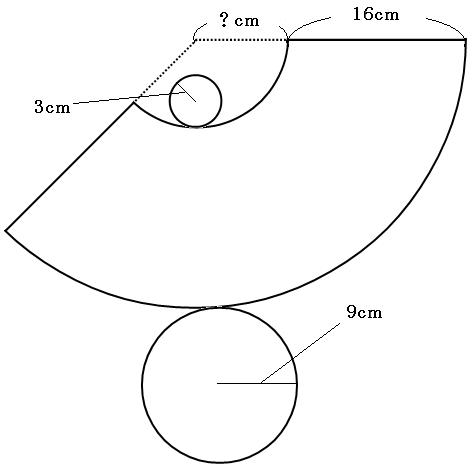
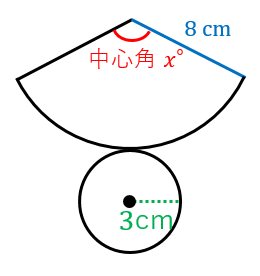
扇形の弧の長さや面積 と中心角の関係を、比 例の見方で考えること ができる。 円錐の展開図をかくと き、側面になる扇 形の 中心角を求めることが できる。 家 円錐の展開図がどのようになるか予想してくる。予習思考 力・表現力・判断力 11漏斗(円錐台)の立体形状から平面の展開図(扇形環)を得る 円錐台の展開図 写真にあるような商品(大きい円の直径3 円錐の展開図の書き方 以下の例題で、円錐の展開図の書き方を説明します。 例題 次の立体の展開図を書け。 STEP1 底面の円を書く まずは底面の円を書きます。 底面は \(3 \ \mathrm{cm}\) なので、コンパスの股を \(3 \ \mathrm{cm}\) に開いて円を書きます。 STEP2 側面のおうぎ形を書く 側面部分を



円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
まず、円錐の展開図は このように、おうぎ形と円が組み合わさった形になります。 そして、ポイントとなるのが 側面であるおうぎ形の弧の長さと 底面である円の円周の長さが等しくなります。 ポイント! (側面の弧の長さ)=(底面の円周の長さ) このことを利用して考えていきます円錐の展開図の扇形の中心角の求め方が解りますか?底辺の半径と母線の長さだけが分かっているのが前提にお願いします。底辺5 、母線10 の円錐。この円錐の展開図の扇形の中心角を求めなさい。こんな問題です 円柱の体積を求めるのが苦手という人が多いんですが、実はたった2つの 三角形Aと三角形Bは相似で、大きさが違うだけ。 故にeは以下で求めることができる。 円錐台の上の円の円周と、展開図の上辺は、同じ長さになるはず。 円周は、直径×円周率で求めることができるから、角度θは以下で求めることができる。 つまり、半径eと半径(ed)で2つの円を描いて、




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
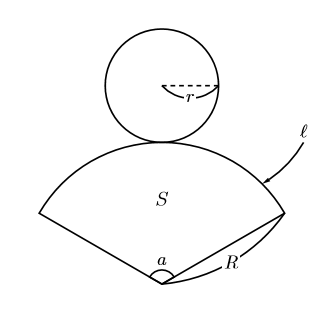



中学数学 円錐関連の公式の導出 数樂管理人のブログ
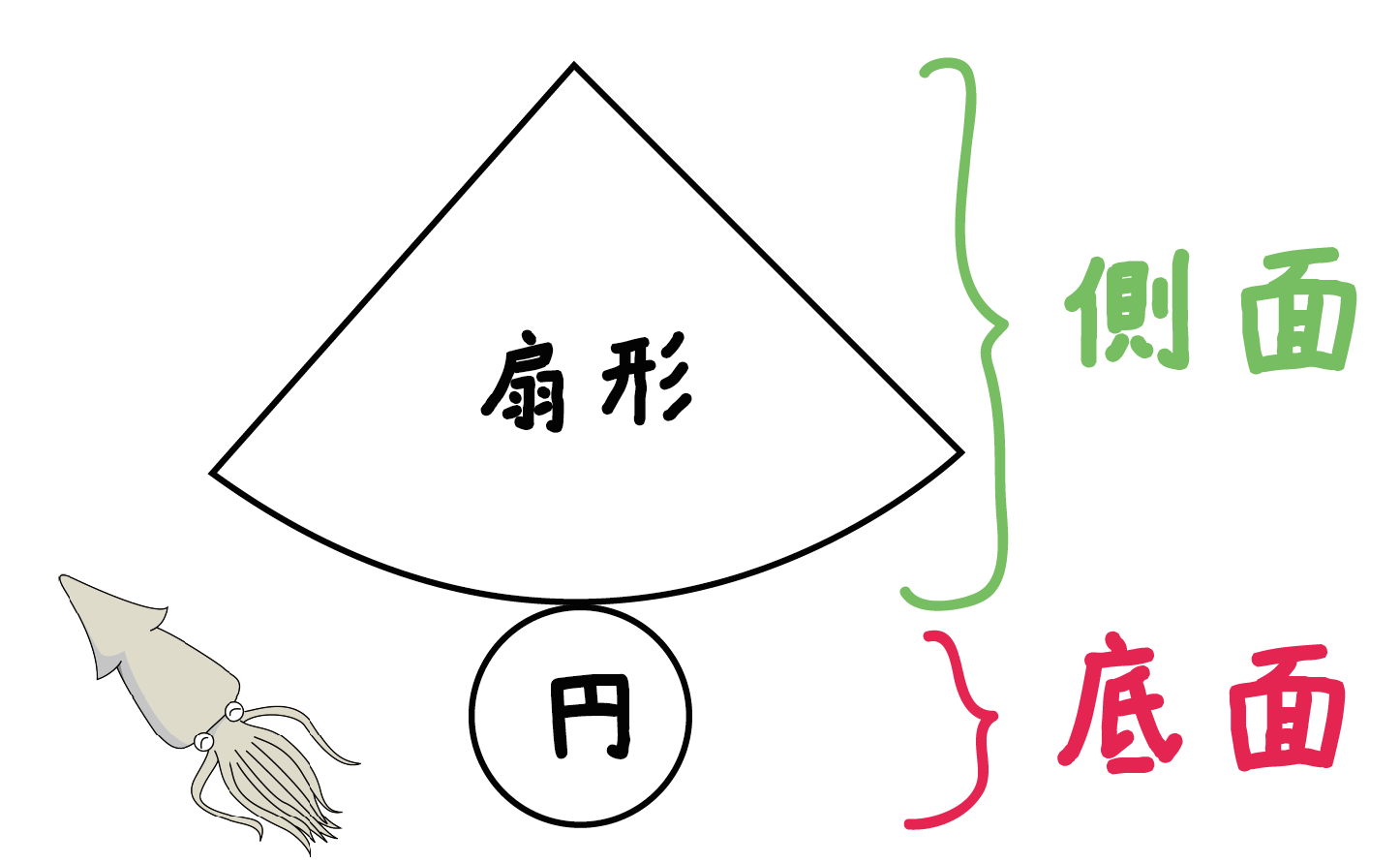
円錐の展開図を描くと、側面は半径24cm、中心角30度の扇形になります。 ひもを2周巻きつけるのですから、その最短経路は、半径24cm、中心角60度 の扇形上で直線(この扇形の弦)になります。 よって、その長さはできる三角形が正三角形なので、扇形の半径扇形の中心角の求め方 (1) 円錐(円すい)の問題ですが、立体と考えず平面で考えればただの中心角の問題です。 覚えておかなければならないのは、円すいの展開図のだいたいの形です。 円すいの展開図は「 おうぎ形 + 円 」です。 そして、大切なことは、
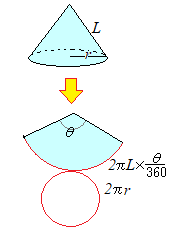



立体の表面積




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



シール屋おやじに喋らせろ デザイン



円錐の側面の展開図の扇形の中心角の公式が360 L Rになるのはな Yahoo 知恵袋




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



円すいと展開図 左上の円すいの展開図がある 円すいの母線の長さと底面の半径の関数として 展開図の次のものを表してみましょう 1 側面 おうぎ形 の中心角の大きさ 2 側面 おうぎ形 の弧の長さ 3 側面積 cabri のデータでは




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



斜円錐電卓その1 1楕円錐展開電卓 2斜円錐展開電卓 Javascript版



Math 円錐の展開図の中心角と母線 半径 中学生 働きアリ




16 号 錐台展開図面作成システムと錐台展開図面作成プログラム Astamuse




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




公式を図解 すい体の体積 円すいの表面積の求め方



円錐台の展開図についてのメモ




円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち



円錐台の展開図についてのメモ




用紙に円錐の展開図 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




円錐の表面積の求め方 公式と計算例



円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
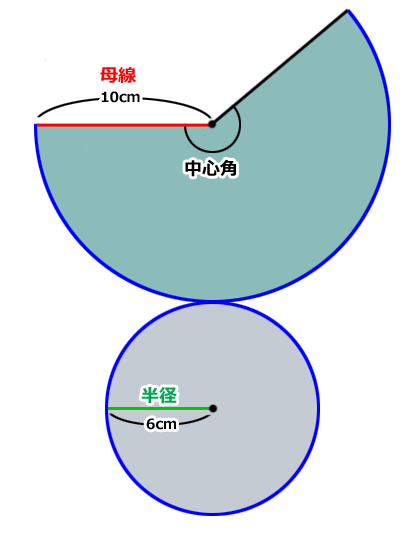



頭の体操 円錐 えんすい の表面積は習った事の応用 13 すべての初心者たちへ オールビギナーズ




円錐の展開図面を描きたい 添付のような円錐の展開図を作りたいのです 数学 教えて Goo




中学数学 円錐の展開図 扇形の面積 底面の半径 Youtube
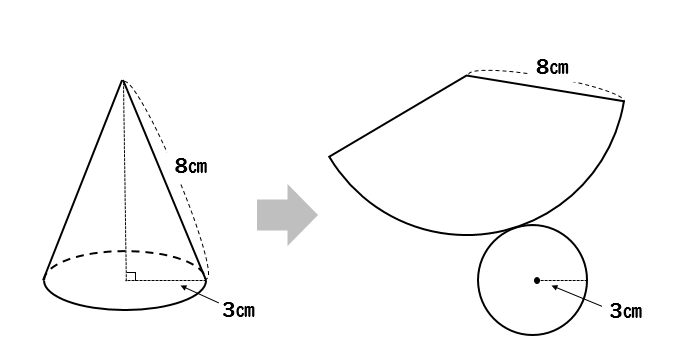



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ



展開図 良い子



中学1年数学です 途中式と答えを教えてください右図の円錐につ Yahoo 知恵袋




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
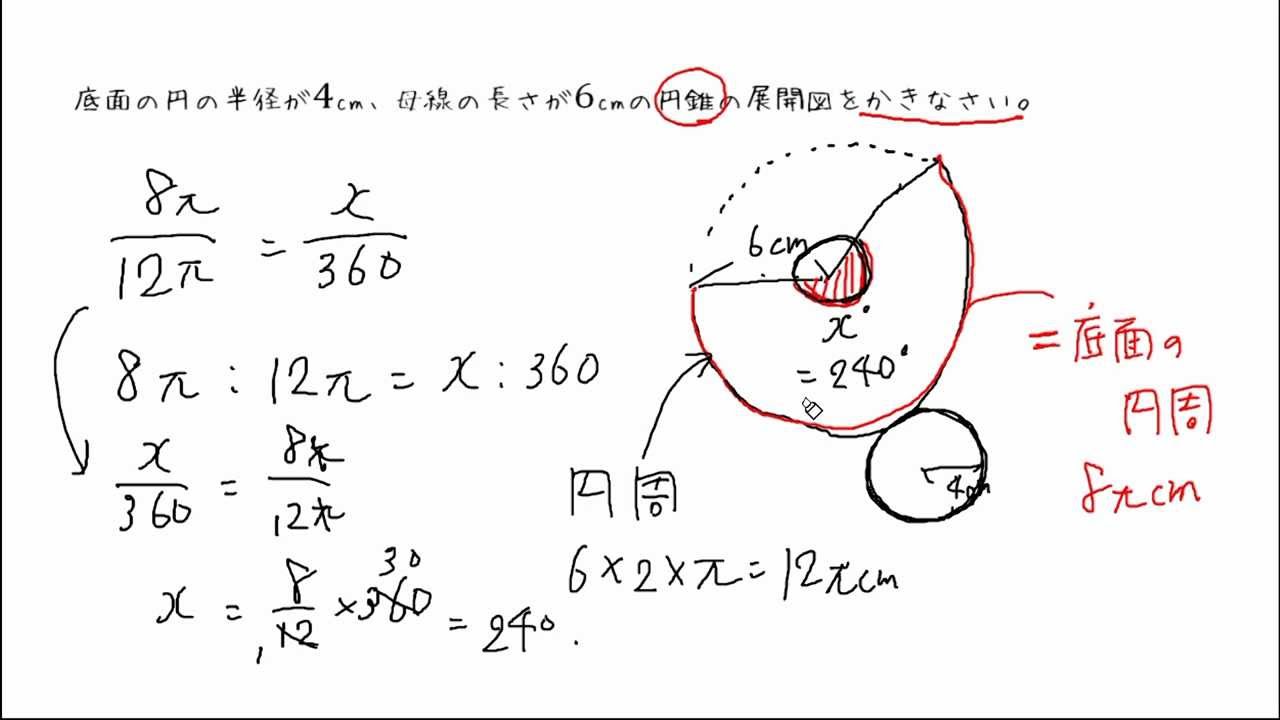



円錐の展開図 Youtube




この写真の円錐の問題で 側面の展開図の扇形の中心角の大きさの求め方 Clear



1




円錐 展開図 書き方 円錐 作図 ハロウィン かぼちゃ イラスト




扇形の中心角の求め方を教えてください Clear




02 号 円錐台状筒体の製造方法 Astamuse
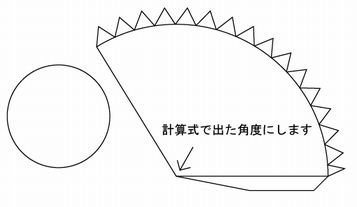



ペーパークラフト初級講座 その3 円柱と円錐を作る ふりぃだむふぁいた




円錐 展開図 ダウンロード ダウンロード に際しましては あらかじめ免責事項をご確認ください 全学年共通 立体の展開図 円錐




円錐の展開図 Youtube




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




円錐台型の展開図フォーム 忘備用 空ike飛行機 Blog
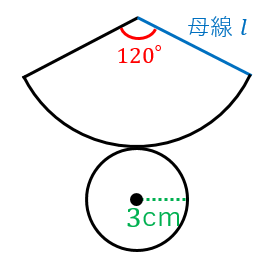



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
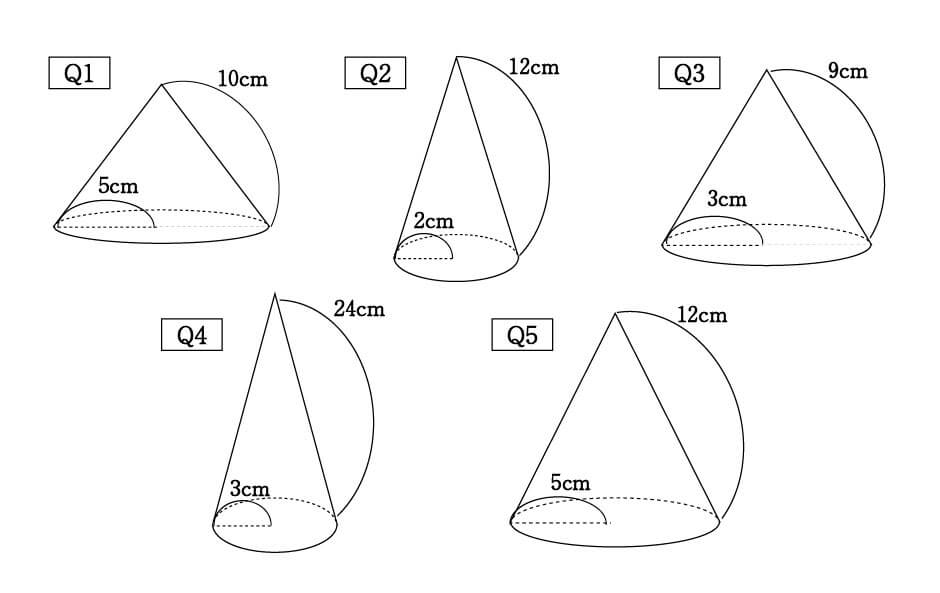



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐をwordで作成 数学教材で使える画像の作り方は 数スタ
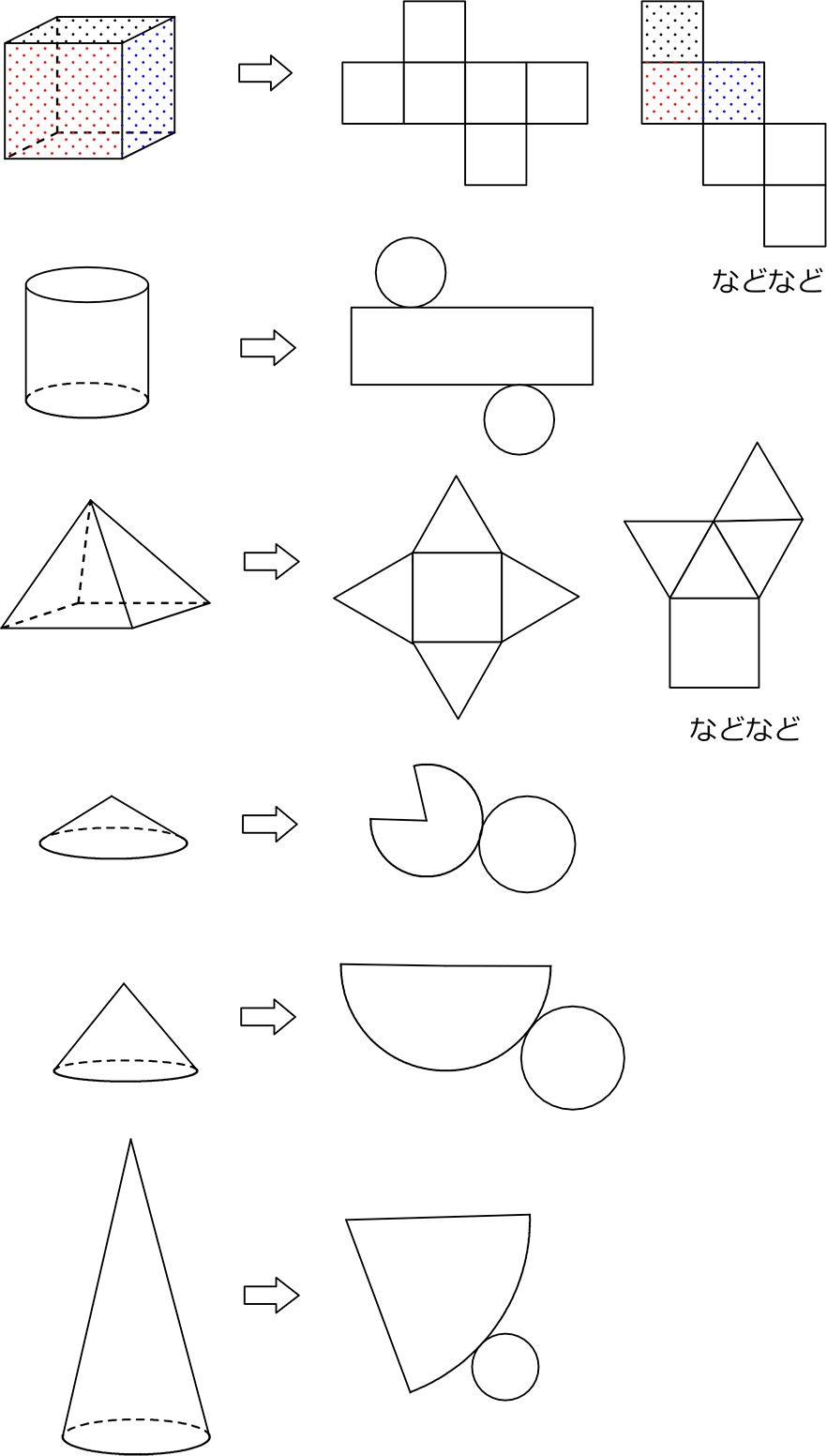



中学数学 空間図形




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




角錐 円錐の体積と表面積の公式 数学fun



漏斗 円錐台 の立体形状から平面の展開図 扇形環 を得る 高精度計算サイト




50 グレア 三角錐 展開図 書き方




久々に頭ひねったw ドールハウス図面づくり 円錐台 くまごろう のブログ
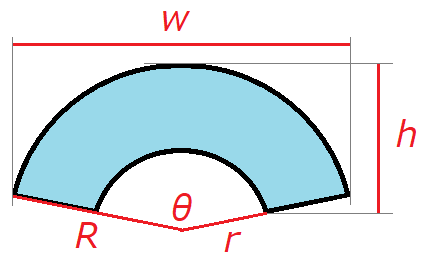



漏斗 円錐台 の立体形状から平面の展開図 扇形環 を得る 高精度計算サイト



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau
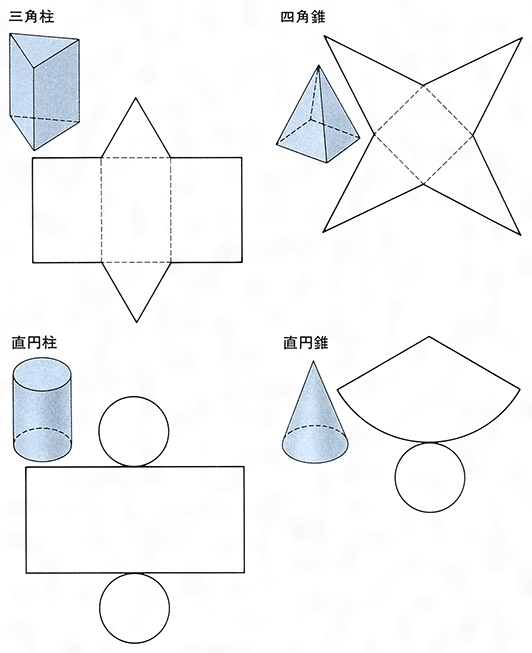



展開図とは コトバンク




直円錐の側面を展開した扇形の中心角 香料ゐっすゐの夢




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張



円錐台の展開図についてのメモ



板金展開プログラム
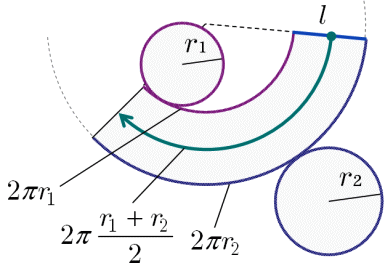



初等幾何 円錐台の側面積を求める 大人が学び直す数学
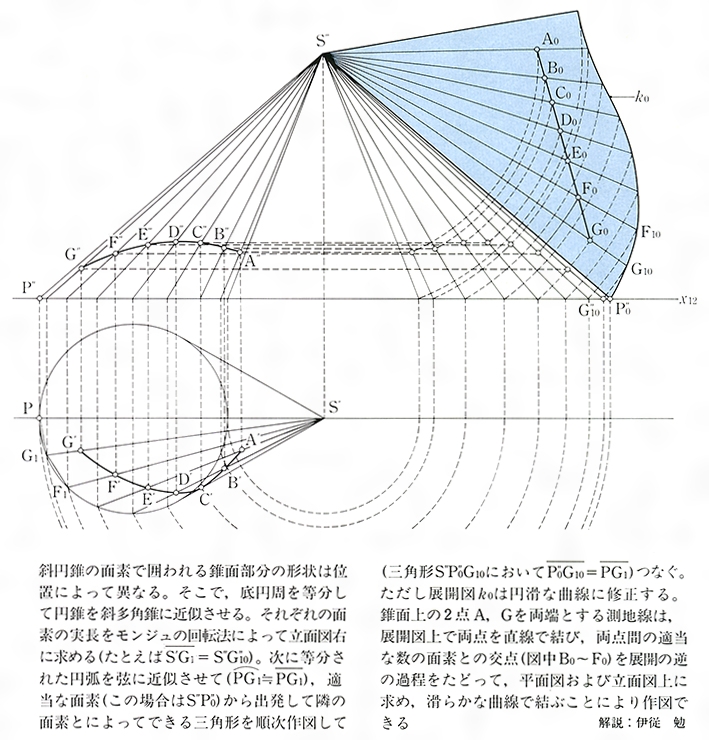



展開図とは コトバンク




円錐の表面積の求め方 You Look Too Cool



円錐台の展開図の書きかたを教えてください 過去の質問を検索してはみたのです Yahoo 知恵袋
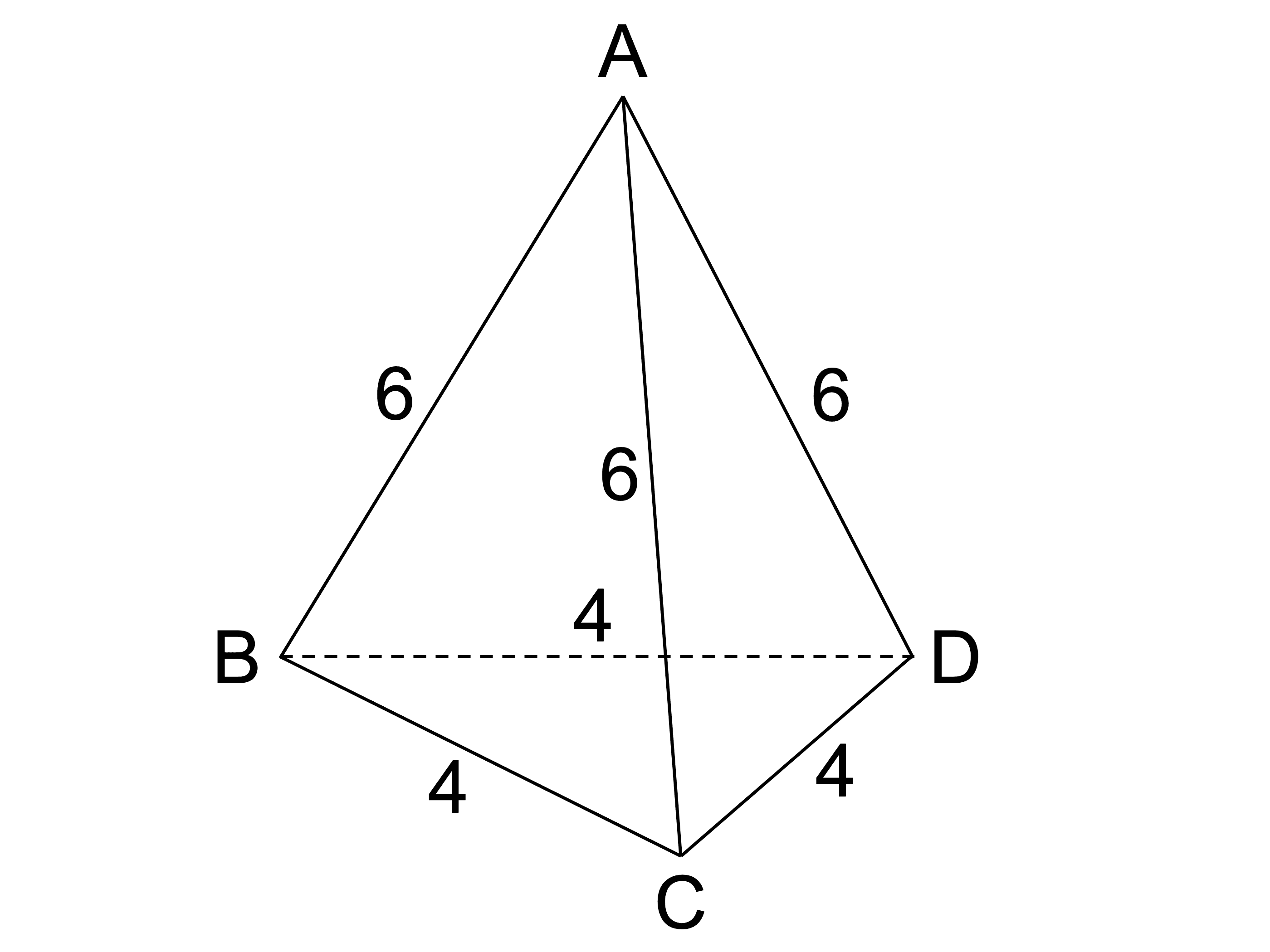



50 グレア 三角錐 展開図 書き方




円錐 展開図 ダウンロード ダウンロード に際しましては あらかじめ免責事項をご確認ください 全学年共通 立体の展開図 円錐




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




円錐の表面積の求め方 公式と計算例




円すいの展開図 中心角の公式を知って5秒で解こう




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Math 円錐の展開図の中心角と母線 半径 中学生 働きアリ
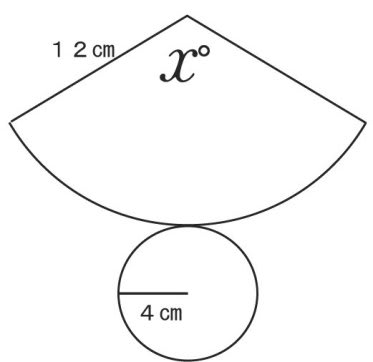



円錐の展開図 の巻き 名寄 算数数学教室より



斜円錐電卓その1 1楕円錐展開電卓 2斜円錐展開電卓 Javascript版




解決済み 円錐面の展開 Autodesk Community International Forums



1




円錐の展開図面を描きたい 添付のような円錐の展開図を作りたいのですが ど Okwave
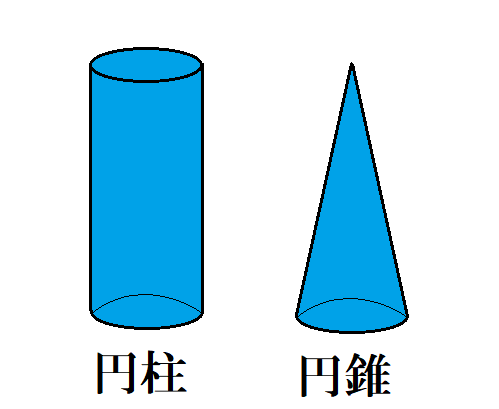



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




円すいの展開図 側面積の求め方 公式を使って15秒で解こう




円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち



斜円錐電卓その1 1楕円錐展開電卓 2斜円錐展開電卓 Javascript版
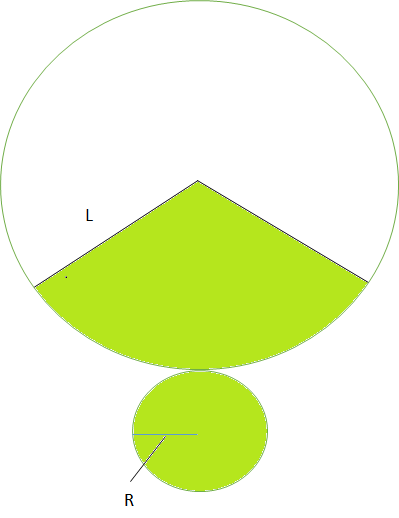



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




扇形の作図の計算方法を教えてください 展開図で扇形 バームクーヘンの一部 Okwave




用紙に円錐の展開図 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
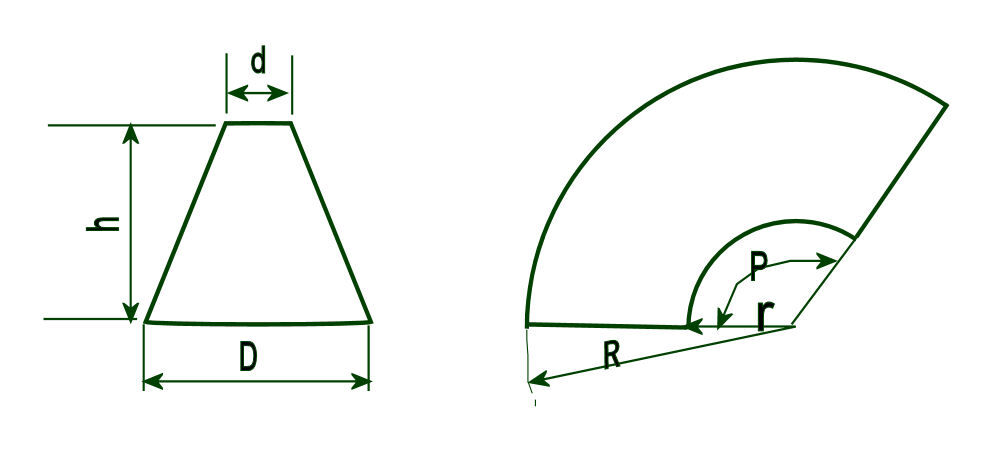



円錐台の作成方法 1 ちょっとしたノーハウ



円すいの表面積の求め方 公式 まいにち一題 中学受験過去問題研究




高校入試対策数学 円錐に関する対策問題 Pikuu




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




扇形 Wikipedia




円すいの展開図 中心角の公式を知って5秒で解こう



楕円 錐 展開 図



0 件のコメント:
コメントを投稿