中学数学のつまずき解消をめざすこの連載。 今回からいよいよ「1次方程式の利用」、つまり文章題に入ります。 方程式の文章問題を解く手順は以下のとおりです。 (1)求めるものを \(x\) とPocket 今回の記事では、中1で学習する一次方程式の解き方についてまとめていくよ! 基本的な方程式の解き方から分数、小数を含む方程式の解き方まで説明していきます。 分数、小数が出てくると難しく思えちゃうんだけど、ある手順をしっかりと踏めば18/2/ 過不足と分配の問題(1次方程式) 投稿日 年2月18日 年12月9日 100sai 方程式を利用して問題を解くときには、問題文の中のどれかひとつの量を として、他の量を を使って表し、それらの量の関係を満たす方程式をつくります。 過不足や分配の問題
求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博
1 次 方程式 問題
1 次 方程式 問題-Ⅰ1元1次方程式について,Ⅱ日常あるいは数学の事象から問題を見いだし,解決の過程を考察 し,伝え合うことを通して,Ⅲ方程式を用いて問題解決できるような力を身に付ける。 2 単元の終末で見取るパフォーマンス評価 パフォーマンス課題 評価基準2.1次方程式の応用 ※解答を非表示にする場合は、このボタンを押してください。 (問1) 次の問題を、方程式を使って解きましょう。 (数の問題) (1) ある数を6倍して2を加え、その値をさらに2倍してから9をひくと55になりました。 ある数はいくつですか。 (2) 9からある数をひき、その値をさらに5倍してから3を加えると28になりました。 ある数はいくつですか



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau
1年生の数学, 1次方程式, 3年生の数学, 受験対策, 文字と式, 正負の数 受験対策問題集(1)中学1年生の数学A 緊急事態宣言延長で塾も休みになったので、中学3年生に課題として出した受験対策問題集の最A B P y=2x18 O x y ある銀行に預金すると1年でx%の利息がつく。 そのままにしておくと次の1年後には利息も含めたすべての預金に対してx%の利息がつく。 A君がこの銀行に8000円預けたら2年後に8405円になっていた。 xの値を求めよ。 ただし、x>0とする。 x = 25,8 x = 1,7 x = 1± 2 2 x = 2± 3 4 x = 17±3 17 2 x = 4,8 x = 2± 5 3 x = 3±2 3 2 a=3, b= 1 2 ①x= 1 2 , ②x=5二次方程式1 ===≪2次方程式の解≫=== 解説 → の応用として, すなわち のような2次方程式も解くことができます. ※この変形方法を使えば,別の頁で扱っている「因数分解による解き方」では解けないような問題でも解くことができます.この変形
28/8/18 1次方程式の利用(2)(整数・過不足・年齢・割合の問題) 10 shun_ei 1800 フォローしました 「方程式で文章題を解く」とは、(1) 求めたいものをxとする 、(2) 等式をつくる 、(3) 方程式の計算方法にしたがって解を求める 、この3つの作業① 問題をよく読み,その意味をつかむ。 そして何をx で表すか決める。 ② 数量の間の関係を方程式で表す。 ③ その方程式を解き,解を求める。 ④ 求めた解が問題に適するかどうかを調べ, 答を決める。 1次方程式の応用 PKP(2226)分数をふくむ1次方程式 (2226a)分数をふくむ1次方程式 解答編 (2229)方程式総復習問題 (2229)方程式総復習問題 解答編 基本的な問題からちょっと複雑な問題まで1次方程式の解き方の練習です。最後は入試問題特集です。 223. 1次方程式を利用して文章題を解く (2241)1次方程式を利用して文章題を解く
例如, n 次方程式 的 n 個根如果是 ,, , ,並且 ,則 很可能是一個很好的預解形, 也可能是一個不壞的預解形, 也是一個預解形(其中任一個 u i 是 a 1,a 2,, a n 的多項式)。 所謂的預解式就是滿足某一預解形的方程式,並且此方程式的求解問題比原來更一般的,我們把數字方程式 推廣成文字方程式 ,其中 a1,a2 ,, an 是沒有任何關係的文字;這種方程式叫做 n 次一般方程式 (the general equation of degree n )。 請注意, x4ax2b=0 不是四次一般方程式,因為 x 項的係為零。 如果我們能夠解一般方程式的根,那麼數字方程式的求根問題當然迎刃而解。 根據 O Neugebauer 的說法,巴比倫人在 1600~1800 BC 已經知道求二次方程式的根3章 1次方程式 2.1次方程式の応用 1方程式を利用した文章題の解法の手順 ①問題をよく読み、わからない数量を\(x\) とおく。 ②等しい数量の関係をみつけて、方程式を作る。 ③方程式を解く。 ④方程式の解が問題に適しているか確かめる。



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau




初中數學重點突破 一元一次方程相關的6類問題 含例題和解析 每日頭條
28/3/21 解けない5次方程式にも実は解法があった? 方程式が「解けない」とはどういう意味なのか 話題の「三体問題」にも関係しています 浅田 秀樹熊本大学数理科学総合教育センター 連立1次方程式の解法 問題1 解答 行列の行基本変形とは • 操作c·i 第i 行をc 倍する • 操作ic·j 第i 行に第j 行のc 倍を加える • 操作i,j 第i 行と第j 行を入れ替える という3つの操作だった連立3元1次方程式とは ・x+y=4 ・x−y=2 この2つの1次式を満たすxとyの値をもとめるには、連立方程式を解けばよかったですね。これまで学習してきた連立方程式は、基本的に文字が2つ、式が2つの組み合わせでした。 今回は、文字




一元一次方程式應用問題 Shareclass



一元一次方程式 測驗01 解方程式 結構數學 國中 發現學習的美麗新世界
25/7/18 今回から、2次方程式を見ていく。 まずは、2次方程式の解き方から始めよう。 前回 ←平方根の補充問題(難) 次回 →2次方程式の解き方(2)(展開、置き換え、二乗の利用)(標) 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二乗利方程式標準問題 1 1 次の方程式を解きなさい。 2x5=9 4x7=1 3x8=5 5x12=3 7x9=19 2x7=13 6x5=13 14x6=15 11=3x4 9=4x7 8=6x1 12=5x2 7=3x13 15=8x11 13=2x35(1) 次の に当てはまる数を書き入れなさい。 t 68 t1 l0を t e Þ ;




解二元一次方程习题




二元一次方程式的解 Youtube
63 l0 ④ t e7 ;練習問題1 次の方程式を解きなさい。 1 x +3=5 2 x +4=-8 3 y -6=9 4 y -2=-7 練習問題2 次の方程式を解きなさい。 1 2 x =8 2 3 x =-9 3 -4 y =16 4 -6 y =-24知④1次方程式の解き方を理解している。 授業観 察 発言 問題集 プリント ノート 確かめよう(1時間) 小テスト ② 1 次 方 程 式 の 利 用 1 1 次方程式の利 用 (3時間) 関④方程式を利用して、具体的な事象の中の問 題を解決しようとする。



韦达定理 一元二次方程根与系数的关系 科普中国



課業輔導中心 一元一次方程式應用題
21/1/17 問題 \(f(x)=x^42x^24x8\) とする。 (1) \((x^2t)^2f(x)=(pxq)^2\) がxの恒等式となるような整数t,p,qの値を1組求めよ。 (2) (1)で求めた\(t,p,q\) の値を用いて方程式\((x^2t)^2=(pxq)^2\) を解くことにより、方程式\(f(x)=0\) の解をすべて求めよ。 コメント 簡単に因数分解できない4次方程式を解く問題です。6 l の形に変形する方法 t 68 t lあ t 68 t eあ1 eあ @ t eあ a 6 lあ (2) (1)の結果を利用して t 68 t1 l0の解を求めなさい。 ⑨ t 672 l0 ⑩ 8 61 l0 ③ t f2 ;次の方程式の整数解をすべて求めなさい. STEP 1 問題の1次不定方程式 の整数解を1つ見つけます.すぐ見つからなければ互除法を利用して求めましょう( 互除法を利用して整数解を求める ). x=2,y=9は 1の整数解の1つです. STEP 2 1にSTEP 1 で見つけ




一次方程式 中1 練習問題あり答えあり 中学生 数学のノート Clear




2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm
第1次方程式の必要性と意味及びその解の意味・与えられた一元一次方程式で解決できる問題 (2) をつくる過程で,具体的な場面と式との対応 関係を的確にとらえることができるように,12/2/ 速度と距離の問題(1次方程式) 投稿日 年2月12日 年12月8日 100sai 方程式を利用して問題を解くときには、問題文の中のどれかひとつの量を\(~x~\)として、他の量を\(~x~\)を使って表し、それらの量の関係を満たす方程式をつくります。1次方程式 axby=c (1) を満たす整数 x, y を求めよ という形の問題を扱う.(不定方程式の整数解とも呼ばれる.) 中学校以来習ってきたように (1)の形の方程式は xy 平面上の直線を表しており,その直線上の点 (x, y) はすべて方程式 (1)の解となっているから,解は無限にある.すなわち不定解になる. この頁では, x, y は整数という条件を付けたときに (1)の解が




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客
15/7/21 方程式文章問題1 中学1年生数学方程式の文章問題です。 買い物であるものを何個かうか、父が子供の年齢の3倍になるのは何年後か? 先に家を出た子供を追いかけた父が子供に追いつくのは何分後か? 折り紙を生徒に配ったときの問題など、方程式の1 次 方程式 問題 2644 1971年美國 Stephen A Cook提出了CookLevin理論,這個數學理論指出任何一個NP裡面的問題都可以在 polynomial time 內,使用DTM,將之化約成「一個布林方程式是否存在解」的問題,這個被化約的問題又稱為布爾可滿足性問題(SAT),我們稱SAT問題為NPComplete問題。 BeanfunLogin New Beanfun OTP login View on GitHub 下載 rar 新楓之谷 Beanfun 登入器 程式下載11/3/ 1次方程式のプリント ① 方程式の解(問題) (解答と解説) ② 等式の性質① (問題) (解答と解説) ③ 等式の性質② (問題) (解答と解説) ④ 1次方程式の解き方① (問題) (解答と



二元一次方程各类应用题 松鼠文库




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download
(1)用消去法來解三元一次方程組。 (2)用三階行列式來表示三元一次方程組的解(克拉瑪公式)。 (3)用平面的法向量或三階行列式來判別三平面的關係。 (甲)消去法 透過假設未知數,解決許多實際的問題會形成解幾個三元一次的方程式的共同 解,以下面的例子來說:第8章 1次方程式の復習 80 はじめに 本章では中学校のときに学習した1次方程式,連立2元1次方程式について復 習します。 しかしながらこれらの方程式をどのようにして解くのか,あるいはどのように 応用するのか,についてはほとんど触れません。五次方程式是一種最高次數為五次的多項式 方程式。 本條目專指只含一個未知數的五次方程式(一元五次方程式),即方程式形如 = 其中,a、b、c、d、e和f為複數域內的數,且a不為零。 例如: = 尋找五次方程式的解一直是個重要的數學問題。




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




ベストオブ一次方程式問題集 ぬりえ壁紙hd
は,連立1 次方程式のAx = b の解の自由度と呼ばれる.この自由度が0,すなわちrankA = n のとき,連立 1 次方程式 Ax = b はただ 1 つの解をもつ. 上記連立 1 次方程式の解の導出について,少し具体的に説明する.例えば 3 個の未知数 x,y,z練習問題1 次の方程式を解きなさい。 1 3( x +4)=6 2 2( x -5)=-4 3 -4 y =-5(3+ y ) 4 y =-2( y -6) 練習問題2 次の方程式を解きなさい。 119/5/8 2年 式の計算総合問題1 2①と②の解答が逆になっていました。4の答が抜けておりました 2 3年2次方程式(因数分解利用)2⑥⑦, 類第1 2⑥, 類題2 2⑥符号間違い 1次関数総合問題Lv3 2②(5,9)(誤)→(5,9)(正)




二元一次方程式應用問題1 Youtube




一元一次方程式應用問題 翰林雲端學院
中学生問題に挑戦! 1次方程式を解こう! 1問目から脳をフル回転させて挑戦してほしい難易度高めの算数問題です。 見た瞬間にパスしそうな気持ちを抑え、少しお付き合いください。 中学校で勉強していたのですから、まったく解けないということはないはずです! この式は「1次方程式」と呼ばれる、あの苦い経験の式です。 しかし、ここでは解き方




初三数学讲义直升班第4讲一元二次方程的特殊根问题 教师版 七七文库www 77wenku Com



1



七年级数学一元一次方程50道练习题 含答案 侵权




一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass




二元一次聯立方程式應用問題例4 5 Youtube
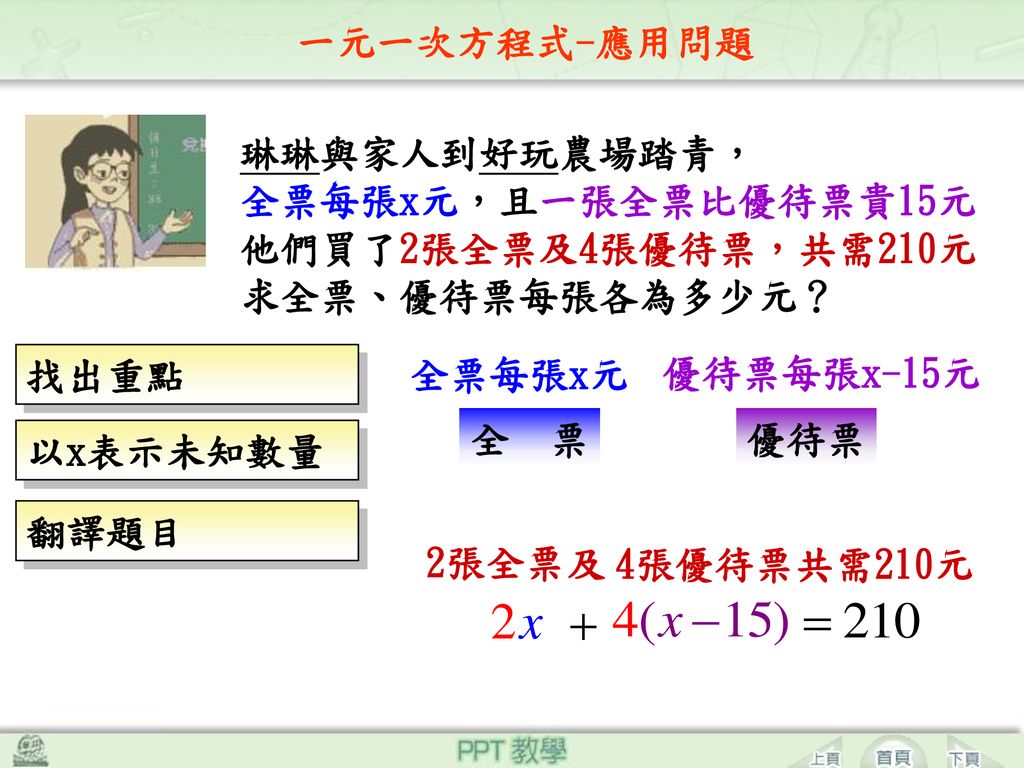



一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download



一次方程式文章問題 かわいいドラえもん



名師課輔網 二元一次方程式時鐘問題




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




一元一次方程式應用問題例1 Amara



Www Boyo Org Tw Boyo Downloads Category 46 17 11 06 01 36 57 Download 32 E5 9c 8b E4 B8 Ad E7 94 9f E4 B8 80 E5 Ae 9a E8 A6 81 E6 9c E7 9a 84 E6 87 E7 94 A8 E9 A1 8c E5 9e 8b E4 B8 E9 A1 8c03 E5 B9 B4 E9 A1 E5 95 8f E9 A1 8c E5 Ad B8 E7 94 9f E7




第三章直线方程式 关于直线的基本问题 一次函数



三元一次方程组解法 哔哩哔哩 つロ干杯 Bilibili



悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答




解一元二次方程式 明誠中學程式設計學習網



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博




1次方程式の解き方2 無料で使える中学学習プリント




3 3 應用問題 一元一次方程式 題庫 Camdemy




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




二次方程式公式解一元二次方程 Ejthgg



Q Tbn And9gctdm2ioiwx1ofwk6oxyprfslnkssmzd2jo K6eubdtv2cctnoej Usqp Cau




隨筆誌 一上3 3一元一次方程式應用問題 一元一次方程式餘數問題




初中数学 一元一次方程常考的13种应用题 掌握考高分 知乎



七年級數學 三道行程問題用一元一次方程或二元一次方程組來解 愛經驗



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博




觀念 一元一次方程式的意義 數學 均一教育平台




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一般 一元一次式 數字易位問題 Youtube



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库




一元一次方程式的應用3 應用問題1 2 解的合理性 Ppt Download




一元一次方程应用题 新人首单立减十元 21年7月 淘宝海外




國一數學 一元一次方程式 求幫忙 十分感謝 Clear




1 次方程式文章題 ニスヌーピー壁紙




中学数学 一次方程式




一元一次方程式的解题方法与技巧 自学习网
.jpg)



隨筆誌 一上3 3一元一次方程式應用問題 父子年齡等差問題




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download
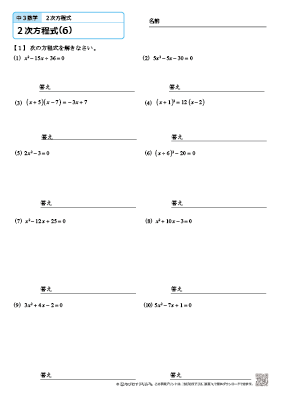



中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



二元一次方程各类应用题 松鼠文库



問題 數學問題一元二次方程式 校園生活哈啦板 巴哈姆特




一元一次方程式應用問題4速率問題 Youtube



Www Cyivs Cy Edu Tw Sub Form Dl Aspx Parser 2 48 469 3453 5




二元一次聯立方程式應用問題 例1 2 3 Youtube




中学数学1年 1次方程式の利用 整数 受験の月




均一影片 例題 二元一次方程式 應用問題3 學習單 Shareclass




最も欲しかった 数学2 次方程式 ニスヌーピー壁紙




中学1年生 数学 無料問題集 一次方程式 おかわりドリル




七年级数学一元一次方程知识点归纳 知乎



名師課輔網 一元一次方程式應用問題人數



Priori Moe Gov Tw Download Textbook Math Grade7 Book1 Math 7 1 8 1 Pdf




一元一次不等式講義新學習指導要領の変更內容の理解 數學 數學a編 Zxmy




一元一次方程应用题典型例题答案 豆知网




三元一次方程题计算题 三元一次方程组计算题题 有答案最好 没有也行 三人行教育网 Www 3rxing Org




1次方程式買い物の文章問題 Youtube




一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント




二元一次方程式應用問題2 Youtube



四年级奥数方程问题 三元一次方程组 四年级奥数题 奥数网




一般 一元一次式 加快速度 待下架影片 均一教育平台



初中数学初一一元一次方程式 学习视频教程 腾讯课堂




基測數學 95v1 單選 一元一次方程式的應用問題 國中基測數學095v1 均一教育平台




我想請問為何二元一次不等式ax By的係數a要大於零 如果題目是給負數我自己要把他變 Clear



二元二次方程式定義連立方程式とは Gjlni




基測數學 96v1 單選24 二元一次方程式的應用問題 國中基測數學096v1 均一教育平台




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア
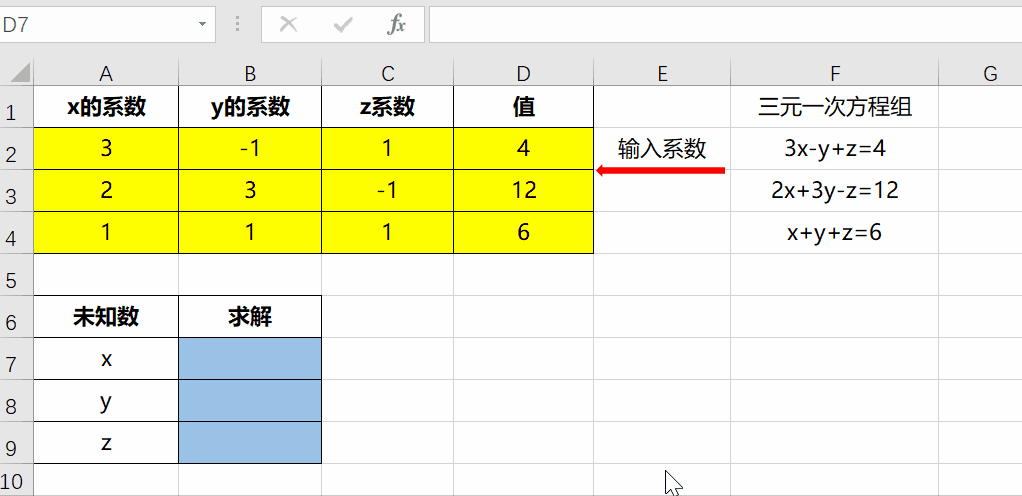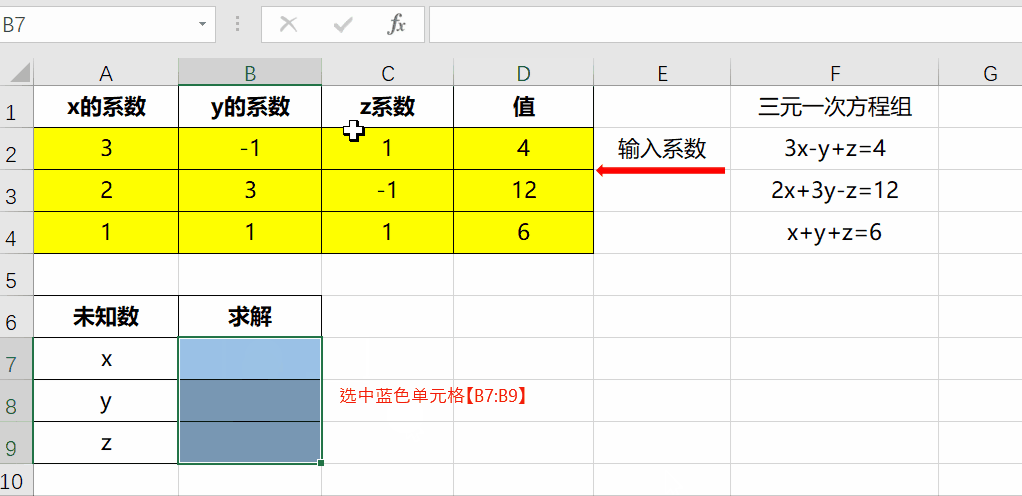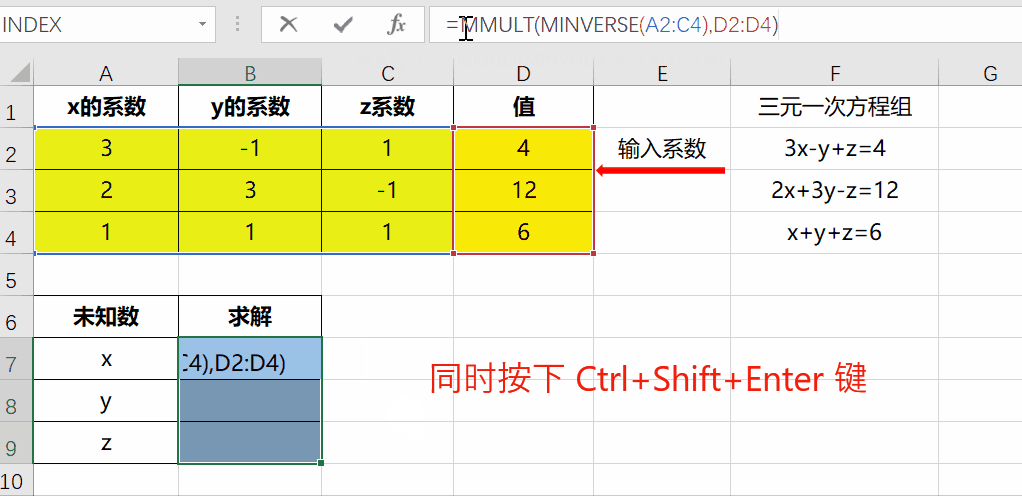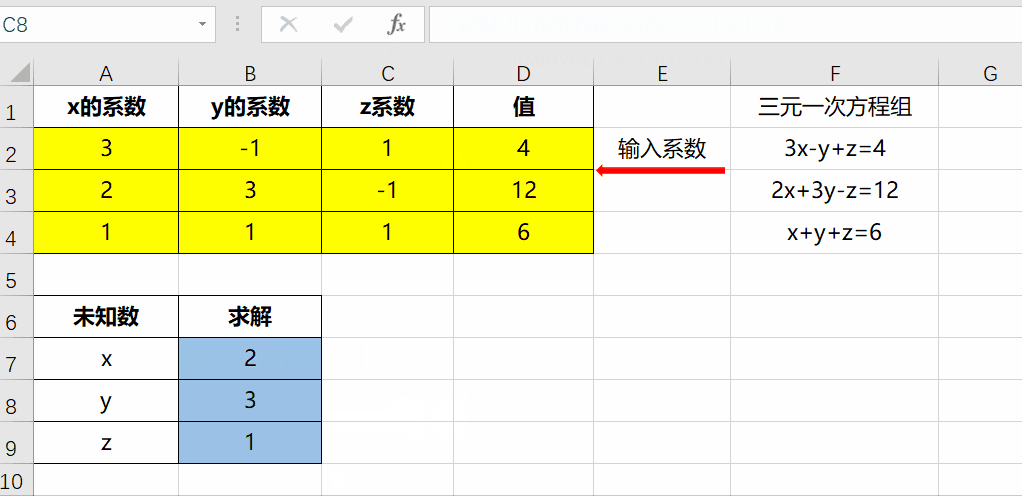



Excel求解多元一次 一元二次方程组就是这么简单 知乎




初中数学 二元一次方程 特别需要注意的问题 考生最好看看 每日头条



完了しました 中1 数学方程式文章題 ニスヌーピー壁紙




連立3元1次方程式 身勝手な主張



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 つロ干杯 Bilibili




一元一次方程知识讲解 经典例题讲解 每日头条
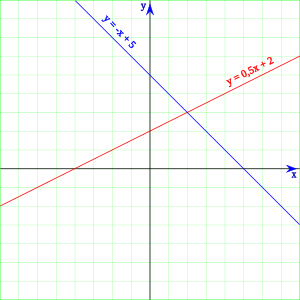



一次方程 维基百科 自由的百科全书




初中數學一元一次方程含參數問題的解題策略 不容錯過 收藏 每日頭條




二元一次方程式及其解的意義 Geogebra




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




一元一次方程应用题 新人首单立减十元 21年7月 淘宝海外




一元一次方程式應用題 1 1 2 Youtube




翻轉學習影片 國中 數學 一元一次方程式 應用問題 練習2




Amazon Co Jp 数学問題集 1次方程式の計算 標準篇 Linear Equations Standard Ebook 柳田 格之進 本




中学数学 一次方程式




國中數學解一元一次方程式 物以類聚篇 Youtube



1




初中数学 一元一次方程常考的13种应用题 掌握考高分 知乎




從大數據思維來準備會考數學科 翻轉教育 親子天下網站




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




一元一次方程式 應用問題閱讀題目解題步驟找出重點以符號表示未知數量翻譯題目 列出方程式 求未知數之值 Ppt Download



0 件のコメント:
コメントを投稿