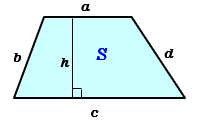
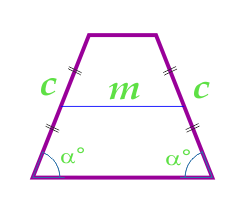
台形の性質 四角形のうちで、一組の対辺が平行なものが台形である。 台形の面積 S の公式として次が知られている。 『 (上底+下底)×高さ÷2 』と、そらんじておられ る方も多いだろう。 教科書等では、通常、次のような形で説明されている。 同じ台形を2つ用意し、下図のように組み合わせて平行四辺形を作る。 平行四辺形の面積の公式から、 2S=(a+b 片側に隣接する角度の合計、180°に等しい台形の特性を使用して、別の式(e d c)= 180°を決定します。 それから、e =(180° 2d)で、公式は(180° 2d d c)= 180°またはc = dの形になります。 6 その結果、角度∠NMO= d = c、∠MNO= e = 180° 2cとなります。角度を求める問題だから簡単とは限りません。 ように決まりますが、 ためには、なんらかの補助線を 引かないと解決しません。 このような整数の角度が与えら れる四角形の問題 を「整角四角形の問題」
1
台形 の 角度
台形 の 角度-台形の角度を見つける方法 科学 21 幾何学では、台形は四辺形(4辺の図)であり、反対側の1組のみが平行です。 台形駆動・三角駆動とは 台形駆動・三角駆動とは、モータを位置決めさせる際の加減速手法のひとつです。 モーションコントロールに於いて、A点からB点に移動させる場合。 計算結果は理論上では限りなく∞(無限大)となりかなりの振動・衝撃となり



等脚台形の角度を求めたいのですが上辺と下辺と高さを入力すれは求められるアプリな Yahoo 知恵袋
Step3 「大きい四角錐」から「小さい四角錐」をひく! 最後は、「大きい四角錐」から「小さい四角錐」をひこう。 そうすれば「正四角錐台」の体積になる。 さっきの例でいうと、 「正四角錐IABCD」から「正四角錐IEFGH」をひけばいいんだ。 地道に計算してやると、 (正四角錐IABCD) (正四角錐IEFGH) = 1/3 × ( 66) × 4^2 – 1/3 ×6 × 2^2友達との目の高さによる目線の角度を計算してみました⭐️ 10 1318 男 / 40歳代 / その他 / 非常に役に立った / 使用目的台形の底辺と面積は下式の関係があります。 A=(ab)h/2 Aは台形の面積、aは台形の上底、bは台形の下底、hは台形の高さです。下図をみてください。 なぜ、台形の底辺と面積が上式の関係になるか示します。まず台形に対角線を引いてください。
α:リード角 I:リード n:条数 P:ピッチ 下の空欄を全て埋めてください。 ねじ種類1台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)(注) 大きな角度の場合、補正ができないことがあります。 (注) 補正すると、画面が小さくなります。 「ピタッと補正」とは? 投写面の正面に置き場所がなかったり、コンセントが届かないなど、斜めヨコからしか投写でき
台形ねじ規格 ・TR:ねじ角度30度で山数はピッチで表す。 ・TM:旧の呼び名で基本的にはTRと同じだが、公差の規格が無い。 ・TW:ねじ角度29度で山数はインチについての山数 左ねじとは 台形の角度と辺の長さの求め方を教えて下さい。 点A、B、C、Dを結んだ台形があります。 それぞれの内角を角a、b、c、dとします。 角a、bは90度であることが解っていますが、角c、dは不明です。 線AB、BC、DAの長さは判明していますが、線CDの長さは不明です。 添付の台形、dの角度が1°になる理由と教えてくださいADとBCを延長して交点をEと置く 台形なのでABとDCは平行なので EDCと EABは相似比1:2の関係にある三角形であるのでED=EC=xであることがわかるので EDC



Q Tbn And9gcqygg7sj1z21o Jerigqs8z2tgc3hvjr Yntmkovzhnmy Edsxh Usqp Cau
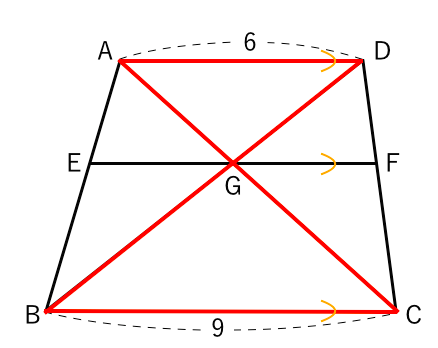



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)等脚台形(とうきゃくだいけい、米語: isosceles trapezoid, 英語: isosceles trapezium )は、台形の一種で、1本の底辺の両端の内角が互いに等しい図形である。 このとき、もう一組の底辺の両端の内角も互いに等しくなる。等脚台形は線対称な図形であり、その対称軸は2本の底辺それぞれの中点を答え 答1. 台形とは、1組の向かい合った辺が平行である四辺形のことをいいます。 答2. 平行とは、ある辺から垂直に線を伸ばした時、その線ともう片方の辺も90°の角度になっている状態のことをいい
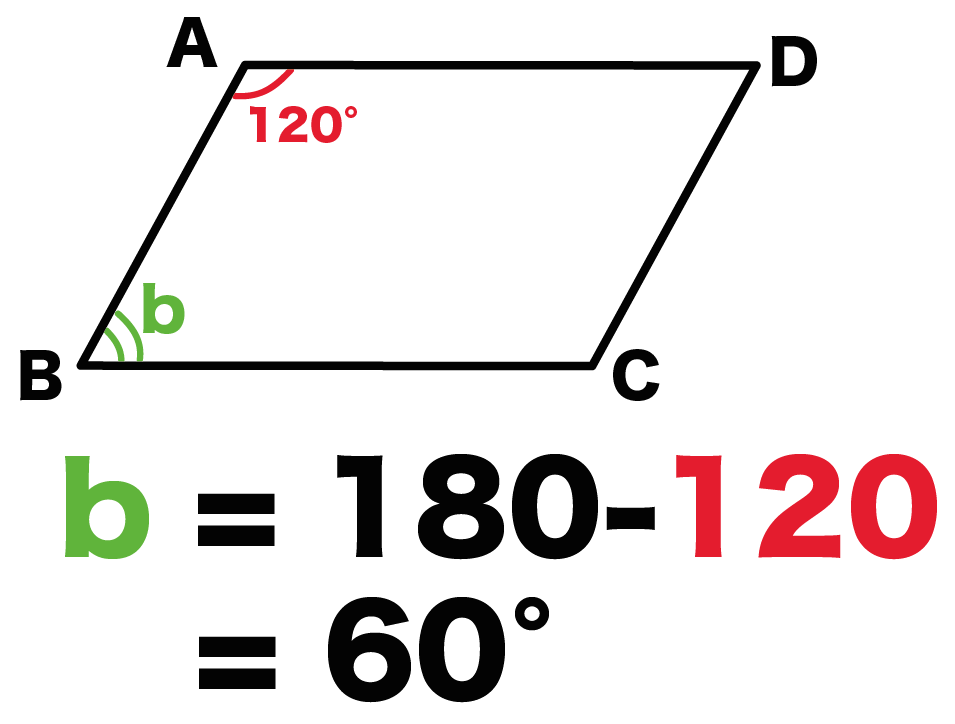



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



等積移動を利用して 台形と平行四辺形 武蔵中学 06年 解けるかな 算数の難問に挑戦
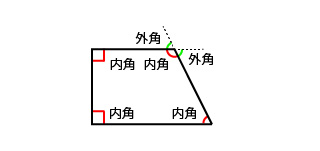
台形,平行四辺形,ひし形 (1)台形と平行四辺形 右の平行四辺形で,辺アイ,アエはそれぞれ何cmでしょう。 また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。 右の図のように三角形の2つの辺でできる角を三角形の「内角」といい、1つの辺を延長して、となりの辺との間につくられる角を三角形の「外角」といいます。 「外角」は三角形の辺の延長の仕方により、違ってきます。 例えば、右の図のように延長線を引くと、 が内角、 が外角です。 この内角と外角との間には次の関係があり、とても重要です。 「三角形の1つ台形(だいけい、米 trapezoid 、英 trapezium )は、四角形の一部で、少なくとも一組の対辺が互いに平行であるような図形である。 平行な2本の対辺を台形の底辺といい、そのうち一方を上底(じょうてい)、他方を下底(かてい)とよぶ。また、もう一組の対辺を台形の脚(きゃく)とよぶ。



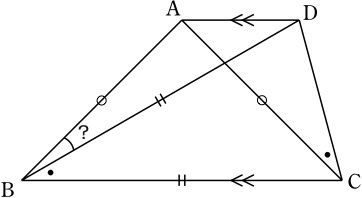
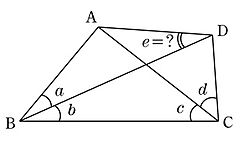
ラングレーの問題 整角四角形



小5 算数 小5 32 四角形の角 Youtube
長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 となります。とても簡単ですよね? しかし これだと面白くないので少し違う考え方をします。 下の図は台形ですが、 この四角形の内角の和を求めていきましょう。ねじの呼び ピッチ P ひっかかり 高さ 基準寸法 (参考) 有効径 6h(M14以下) 6g(M16以上) ピッチ 細目 P ひっかかり公式の考察 なぜ? 台形の面積の公式が「 上底 下底 高さ ( 上 底 下 底) × 高 さ ÷ 2 」になるのかを考えてみましょう。 「赤色の台形」と同じ形の「青色の台形」をひとつ用意します。 「青色の台形」をひっくり返して、「赤色の台形」とくっつけると 平行四辺形になりますね。 平行四辺形の面積を求める公式 は 平行四辺形の面積 底辺 高さ 平 行 四 辺




雑記 分からないことを 悔しい と感じることは大切だと思った話 台形の内角の話 算数 数学 の文章題 特殊算など のことを書くページ
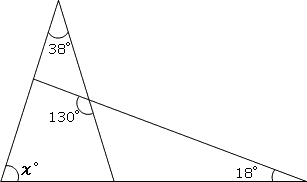



角度の求め方 算数の教え上手 学びの場 Com
ネジ山の角度が60度でピッチで表す ウイットネジ(吋目) ネジ山の角度が55度で山数で表す ユニファイネジ ネジ山の角度が60度で山数で表す 台形ネジ(tr・tmネジまたは梯形ネジ) ネジ山の角度が30度でピッチで表す 角ネジ ネジ山の断面が正方形に近く山数で表す台形ネジとは ねじ山の形が台形をしているねじ。ねじ山角度が 30°のものと 29°のものが jisに規定されている。前者はメートル系ピッチで,後者はインチ系ピッチのアクメねじの流れを受けたものであD2:ねじ軸有効径 ⇒台形ねじ仕様表より d :ねじ軸リード角(度) ⇒台形ねじ仕様表より n 1:ねじ軸毎分回転数(min-) 3ねじ効率η η=1-μtan(d) 1+μ/tan(d) μ:動摩擦係数 d :ねじ軸リード角(度) 4負荷トルクT(N・cm) T= FS・R 2π・η




台形の 面積 底辺 角度 から 上辺と高さ の求め方 台形の面積 数学 教えて Goo



角度の求め方 算数の教え上手 学びの場 Com
タイミングベルト(台形歯) タイミングベルト (台形歯形) ―g‐2― タイミングベルト タイミングベルトは、チェーンやギヤの場合と同じように、噛合いの原理を 応用した定角速度運動を行い、同期伝動をする ベルトです。 特 長 用 途




数学 中2 53 角度チャレンジ Lv 1 Youtube




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Http Www Hpa Kb Site Com Wp Content Uploads 15 02 E5 B9 E9 9d E5 9b E5 E8 92 E5 Ba A6 13 Pdf



角度の求め方 算数の教え上手 学びの場 Com




台形の任意の高さにおける上辺の長さ 相似関係の2つの台形の高さがそれぞれ Okwave




台形の面積の求め方 公式と計算例



三角比を用いた面積計算をマスターしよう スタディクラブ情報局




算数角度問題 ヒラメキを要する角度を求める良問 Youtube



ラングレーの問題 整角四角形



図形ドリル 第96問 等脚台形と三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



計算




斜め等辺台形は 10 であり 台形ベースで 60 度の角度を形成します 台形の中心線を見つけます のイラスト素材 ベクタ Image



1



ラングレーの問題 整角四角形



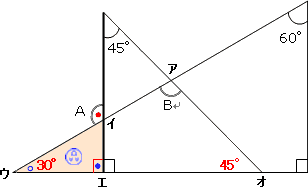
幾何大王からの挑戦状 角度の問題 4



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




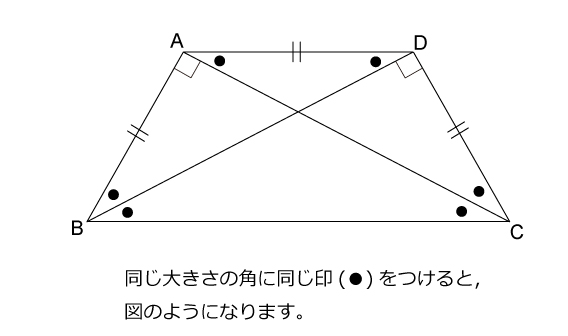
等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



台形の面積の計算 もう一度やり直しの算数 数学




ロイヤリティフリー四角形 角度 求め方 最高のぬりえ




台形補正機能 オートキーストン 台形歪み補正 について



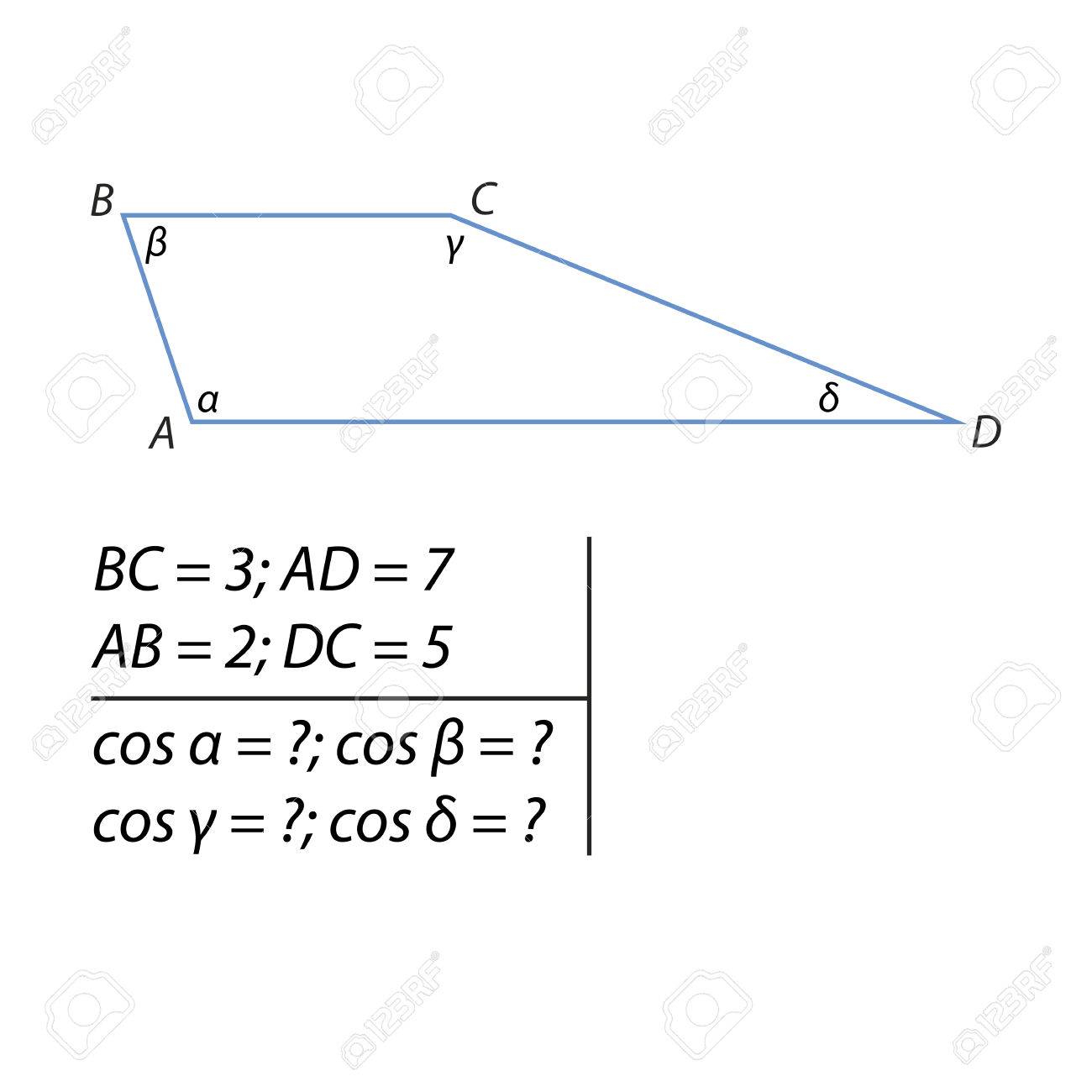
台形の角度 図のような台形において上底 下底 高さが指定 Yahoo 知恵袋



長方形の計算 もう一度やり直しの算数 数学



1



心に強く訴える台形 の 角度 最高のぬりえ




等脚台形において 2本の対角線の長さが等しいことの証明 うさぎめし C
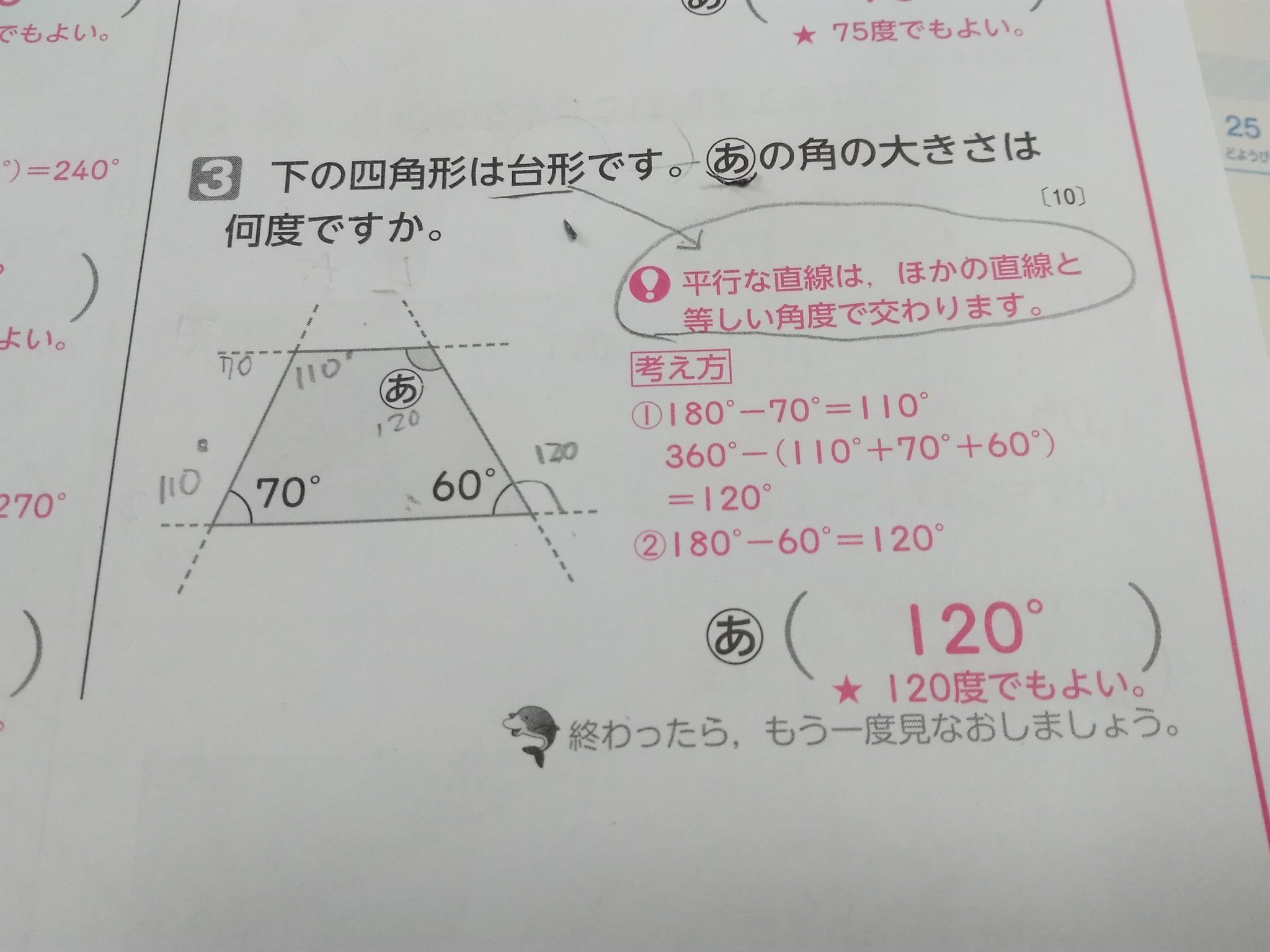



Megi メギ En Twitter 学校テストのこの問題 台形 は1組の平行線が含まれるのが前提で 模範解答にも 平行な直線は他ほかの直線と等しい角度で交わります 書いてあるのに なぜに平行線の錯覚じゃなくて 四角形の内角の和から差し引いているのかな 誰か教えて



等脚台形の角度を求めたいのですが上辺と下辺と高さを入力すれは求められるアプリな Yahoo 知恵袋




小5 算数 小5 32 四角形の角度 Youtube



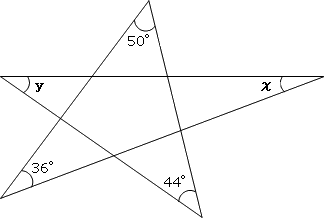
ラングレーの問題 Wikipedia




台形の面積




台形の面積




台形の 面積 底辺 角度 から上辺 高さを計算したい その2 先 数学 教えて Goo



Q Tbn And9gcsg Imfxghclql 9gdv G90aaxy9ysvqu Octrlhncwv1svapu Usqp Cau
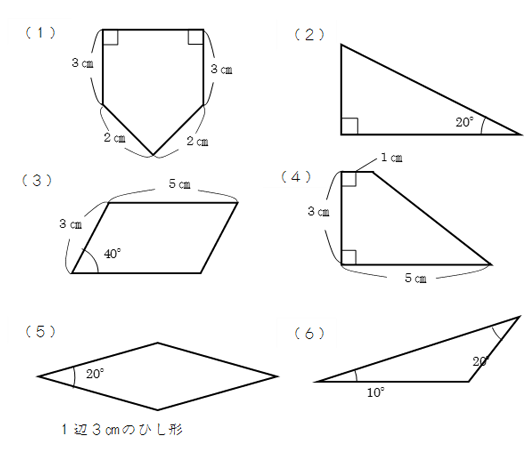



第22回 図形の切り分け いろいろな形に切る 算数ドクター




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
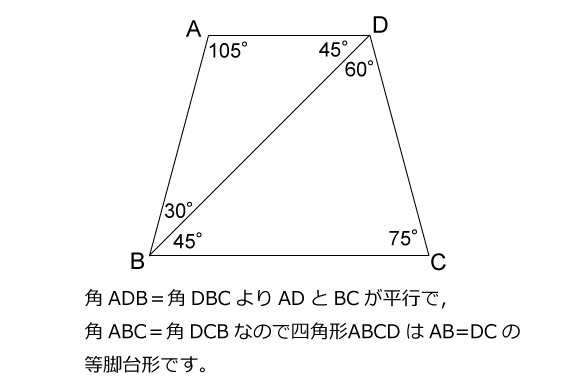



図形ドリル 第256問 四角形と対角線 算数星人のweb問題集 中学受験算数の問題に挑戦



台形の内角の和は360 ですよね 台形に対角線を1本引い Yahoo 知恵袋




角度の求め方 算数の教え上手 学びの場 Com
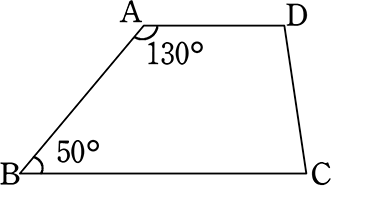



中学数学 平面図形と平行線の性質



台形の角度の計算を教えて欲しいです 台形は画像のような中心から Yahoo 知恵袋



添付した図のような台形の xの角度を求めようと思っています 参 Yahoo 知恵袋
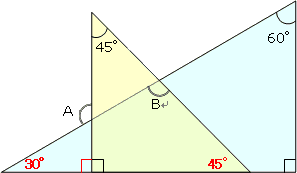



角度の求め方 算数の教え上手 学びの場 Com
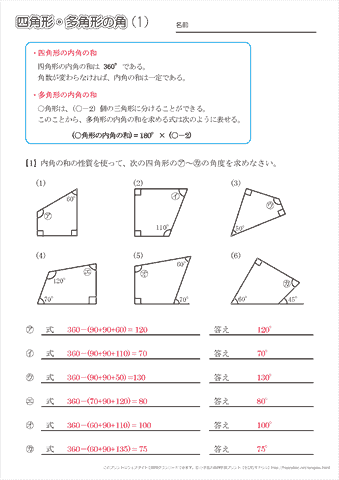



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



四角形の対角線の角度 ラングレーの問題 中学数学の難問図形問題 受験数学かずスクール



角度の問題




小学校5年 算数 四角形の内角の和 Youtube



台形の面積
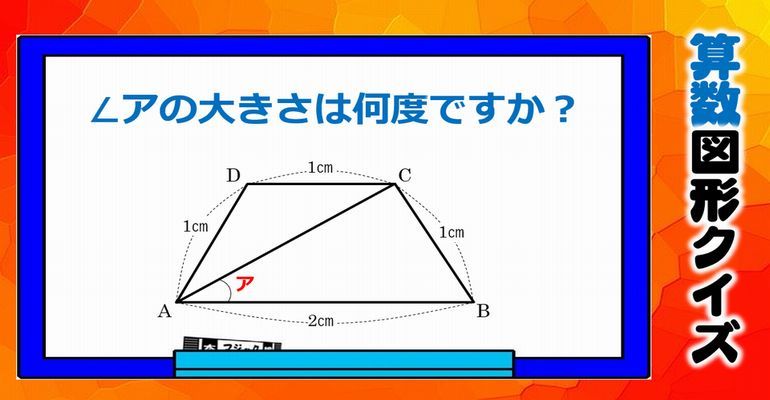



算数図形クイズ サクッと解きたい標準レベルの角度問題 子供から大人まで動画で脳トレ 楽天ブログ




至急でお願いします 台形はなぜ線対称じゃないのか教えてください Clear




Aの角度が知りたい 図の台形のaの角度が知りたい 計算方法を教えてく Okwave




台形と平行四辺形の定義 ちがい 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
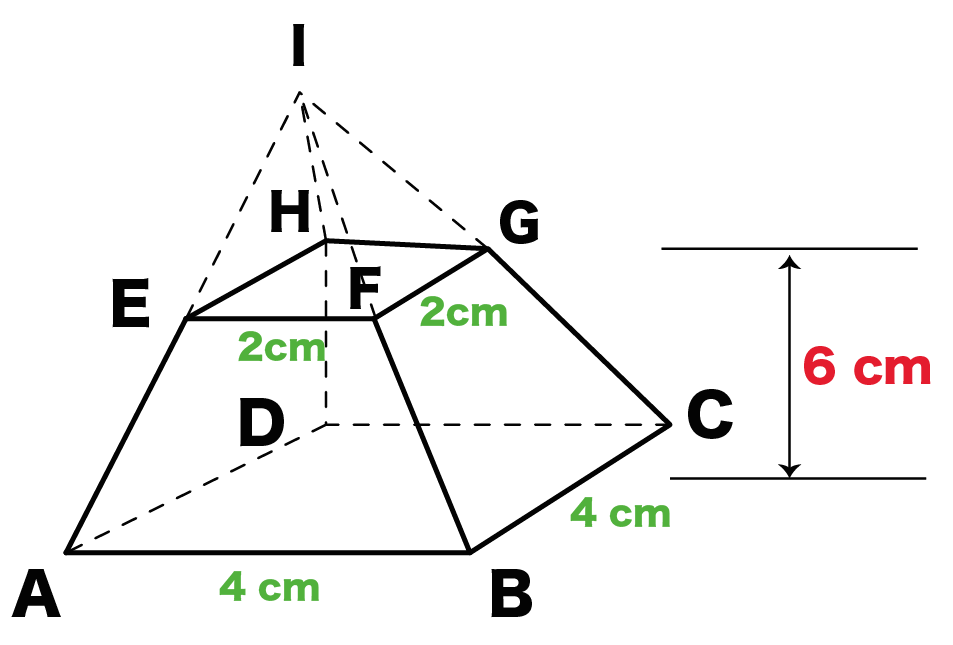



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
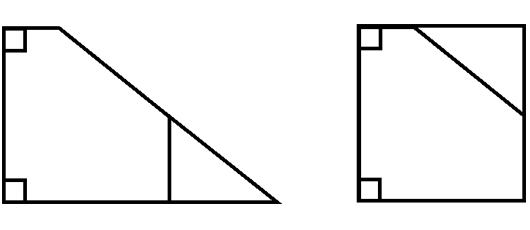



第22回 図形の切り分け いろいろな形に切る 算数ドクター




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch



小4算数の宿題です の角度を分度器を使わずに求める問題です Yahoo 知恵袋




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



角度を教えてください 台形は 四角形の一部で 少なくとも Yahoo 知恵袋



角度問題より 台形を折った角度 城北中学 2010年 これが中学入試に出た図形問題




3242 039 角度 等脚台形 解答 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱




小4算数 Aと同じ角度はどれ 垂直と平行といろいろな四角形 台形 平行四辺形 ひし形 の解き方 教え方 いっしょに勉強しよ
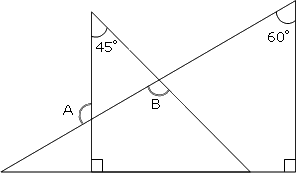



角度の求め方 算数の教え上手 学びの場 Com
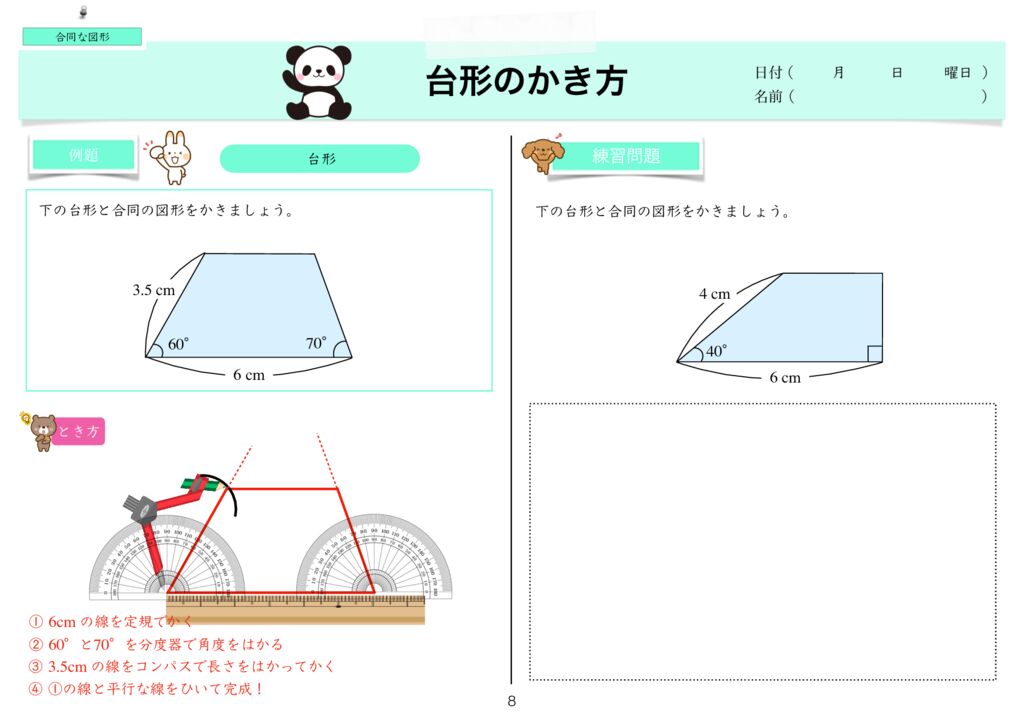



台形のかき方



ラングレーの問題 整角四角形



補助線の練習




オートシェイプ 台形 パターン角度 オレンジ テンプレートのダウンロードはbizocean ビズオーシャン




角度の超難問 解答編 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法




角度の求め方 算数の教え上手 学びの場 Com



数学 画像の図形の角xの角度の出し方を教えてください 台形の向かい Yahoo 知恵袋
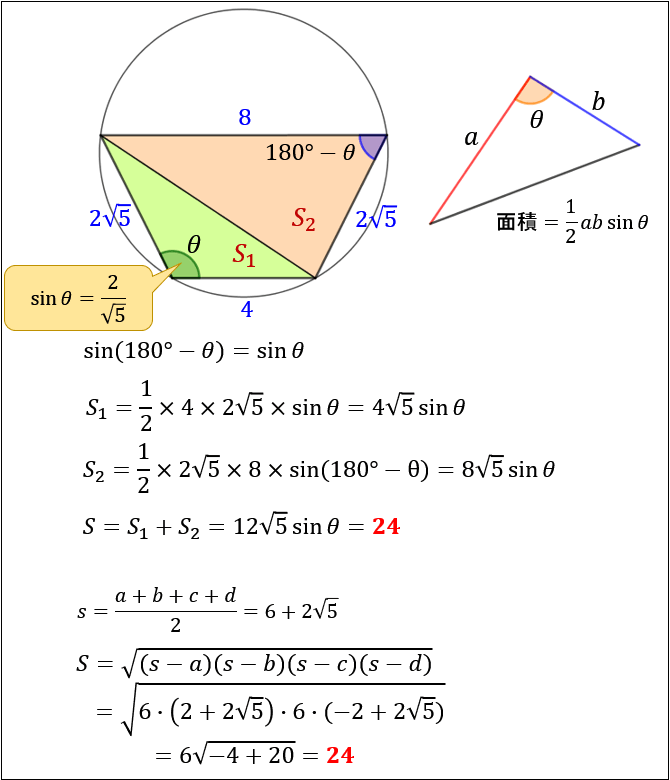



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




四角形の角度の求め方 昔求め方習ったんですが 忘れたので教えてくだ 数学 教えて Goo
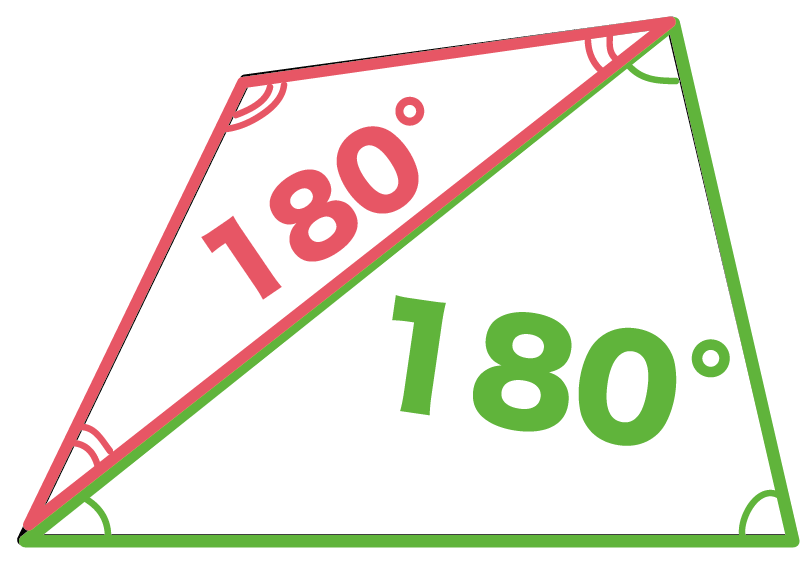



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



図形の問題です 角度を求めてください 台形abcdに 対 Yahoo 知恵袋




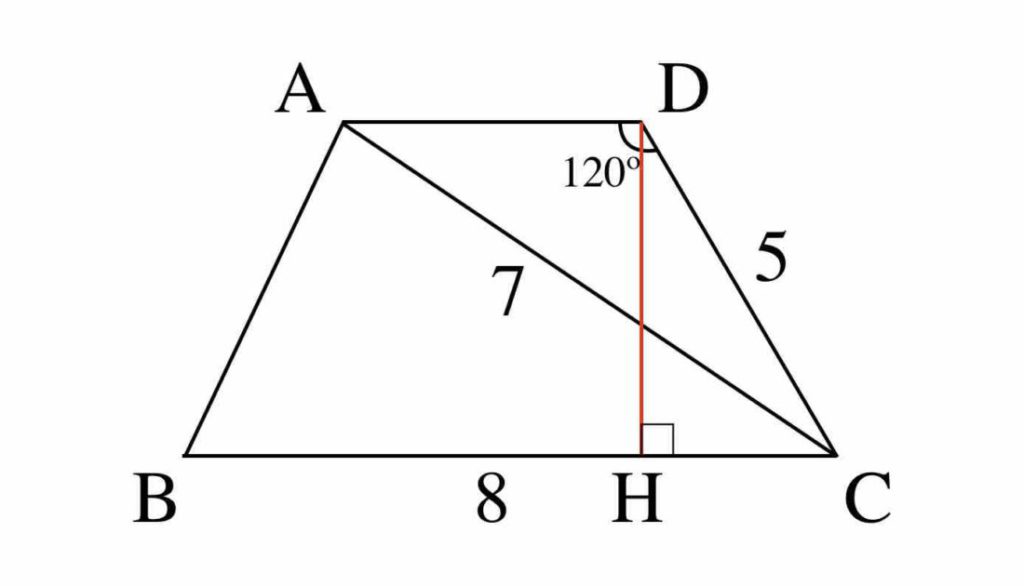
台形の問題がわかりません 教えてください 数iの範囲のようなので 数学 教えて Goo



Http Sansutp Com A10 11 Pdf




台形の面積の求め方 公式と計算例




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
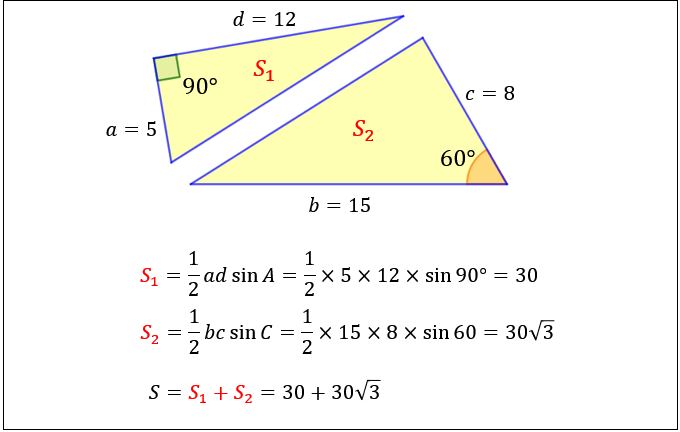



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
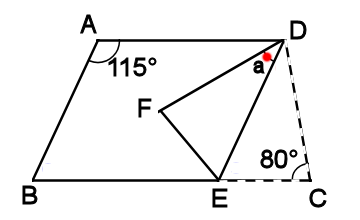



台形を折って



台形の角度の求め方で質問があります Xとyの角度を教えて頂ければと思います Yahoo 知恵袋




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




数学 台形 角度の問題教えて 添付の台形 Dの角度が1 になる理由 数学 教えて Goo




仕事で 高さの分からない台形の面積を求めないといけません Okwave




重要 等脚台形とは 円と関係する定理も Youtube



横浜雙葉11 1 の 4 角度 台形を折り曲げてできた角の大きさを求める問題 気まぐれ解説カフェ 仮
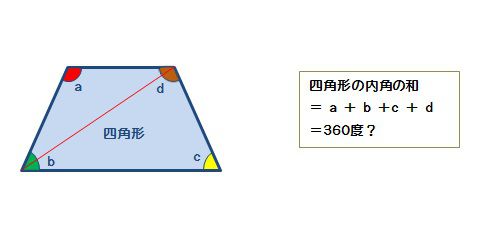



四角形の内角の和 算数の公式覚えてますか




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
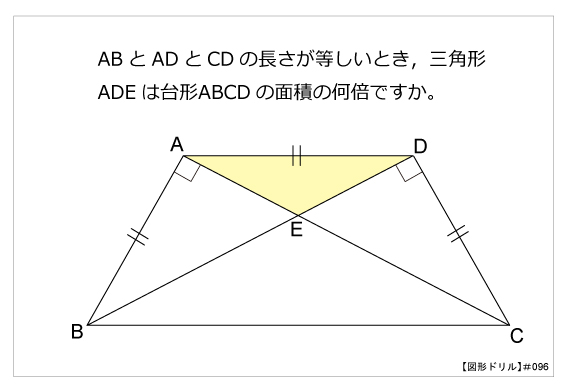



図形ドリル 第96問 等脚台形と三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



幾何大王からの挑戦状 6 Spiral World別館



Basic A 等脚台形 補助線



台形の角度abcdを求めて下さいm M円に内接などはしていないです Yahoo 知恵袋



台形の角度調整はどうやるのでしょう Powerpoint07を使用 Okwave




台形の面積の求め方 公式と計算例




角の大きさを求める 中3模試の超難問 わさっきhb



0 件のコメント:
コメントを投稿